Small a world: Small World: Маленький мир | Купить настольную игру в магазинах Hobby Games

Содержание

Маленький мир / Small World

Маленький мир (Small World) – это стратегическая игра о борьбе фэнтезийных рас, старающихся завладеть древними землями своих предков.

Игра Small World проходит на карте вымышленного мира с холмами, горами, озёрами, равнинами, болотами и лесами. Для каждого числа игроков предусмотрена своя карта. В начале первого хода игрок выбирает расу, которой будет управлять. У каждой расы есть два особых свойства: основное расовое и вторичное случайное. Так, например, могут получиться летающие амазонки, водоплавующие орки или лесные тритоны. Сочетания свойств создают разнообразие как в ходе каждой отдельной игры, так и от игры к игре.

В свой ход игрок либо развивает свою активную расу, либо, если ему кажется, что раса уже достаточно ослаблена другими народами, позволяет ей угаснуть и выводит новую расу. В любом случае, ни одна раса никогда не будет достаточно многочисленной, чтобы захватить все земли. Важно не пропустить момент, когда активная раса теряет потенциал роста: тут игроку надо сбросить её, смириться с её упадком и ввести в игру новую расу.

При этом старая раса продолжает контролировать области, оставляя на них по одному своему жетону. Новоприбывшая раса должна начать захват с крайних регионов. Для захвата используются жетоны расы. Везение в игре почти ничего не решает. Чтобы захватить область, необходимо затратить 2 жетона за пустую область и ещё 1 за каждый жетон чужой расы или защиты в области. После того, как запас жетонов истощится, игрок может перегруппировать жетоны между занятыми регионами. В конце хода игрок получает одну победную монету за каждую контролируемую область и может получить дополнительные монеты за расовое и вторичное свойства. Победные монеты тратятся на приобретение новых рас. Игра длится от 8 до 10 ходов. Побеждает игрок, набравший наибольшее количество победных монет.

Компания Days of Wonder выпустила шесть дополнений для игры Small World, которые содержат новые расы и свойства. Также существует бесплатные расширение, позволяющее играть на генерируемом из гексов поле, и официальный сценарий Necromancer Island.

Обратите внимание при смешивании разноязычных версий игры и её дополнений: карточки рас/способностей во французской локализации имеют место для соединения с другой стороны.

A Small World: «частное» онлайн-сообщество

Харви и Боб Вайнштейн известные личности в Голливуде. Благодаря их поддержке, в первую очередь финансовой, мир увидел такие картины, как «Криминальное чтиво», «Умница Уилл Хантинг», «Бесславные ублюдки», «Чтец» и десятки других. Однако несколько лет назад Вайнштейны сделали необычную для себя инвестицию — вложились в онлайн-сообщество под названием A Small World.

По сути, это закрытый клуб, какие есть во многих городах по всему миру, но расположенный в интернете. Далеко не каждый может стать членом A Small World; необходимо иметь связи, образование, положение в обществе и, конечно, не помешает хороший счет в банке. К примеру, участниками сообщества являются Наталья Водянова и Наоми Кэмпбелл.

Для братьев подобное вложение было единственным в области интернет-технологий, однако Вайнштейны сами собой олицетворяли идеи и дух A Small World. Тем удивительнее была новость о том, что в 2009 году Харви и Боб продали закрытую социальную сеть молодому бизнесмену Патрику Лиотар Вогту.

Патрик Лиотар Вогт

Патрик занялся преобразованием A Small World. Благодаря мероприятиям, на которые Вогт регулярно приглашает своих друзей в лице Оливии Уайлд, Дерека Бласберга и других небезызвестных личностей, про A Small World узнали жители десятков стран.

Несмотря на набирающую обороты популярность, социальная сеть не планирует расширяться: «Понимаете, особенность A Small World в том, что мы не гонимся за количеством пользователей. Главное для нас — собрать единомышленников, чтобы каждый участник сообщества был уверен в человеке, с которым вступает в диалог. Именно с этой целью мы поставили ограничение по максимальному количеству участников — 250 тысяч человек и ни одним больше,» — говорит Патрик Лиотар Вогт.

Подробнее о том, какими принципами руководствуется онлайн-сообщество, подбирая новых участников и чем A Small World принципиально отличается от Facebook, бизнесмен рассказал Buro 24/7.

Леа Сейду и Оливия Уайлд

Проект A Small World не очень известен в России. Расскажите о нем подробнее.

A Small World был основан шведским графом в 2004 году в качестве закрытого сообщества для узкого круга лиц. В мае этого года проект был перезапущен. Теперь он дает возможность членам сообщества организовывать свои путешествия и в целом регулировать образ жизни, используя хорошие связи, получая советы и помощь от участников A Small World.

Члены сообщества — это, условно, «инсайдеры» в разных странах. Когда вы собираетесь отправиться в путешествие, то находите человека, проживающего в нужной вам точке на карте, и он предоставляет вам всю необходимую информацию. Учитывая, что мы принимаем в сообщество людей по определенным критериям, то чаще всего человек, с которым вы общаетесь, помимо информации будет готов дать вам доступ в закрытые заведения своего города.

Еще одним нововведением последнего времени стало мобильное приложение. Учитывая формат, в котором мы работаем, очень удобно общаться посредством мобильных гаджетов.

Помимо строго отбора участников, чем еще отличается от всем известных социальных сете, например, Twitter и Facebook?

A Small World гораздо больше, чем просто социальная сеть. Правильнее назвать нас мировым сообществом, клубом. Facebook, в первую очередь, удобен для коммуникации с родными и друзьями. A Small World позволяет общаться с совершенно незнакомыми людьми, имея при этом гарантии того, что вас не пытаются обмануть.

Доверие — вот наша главная отличительная особенность. Мы проверяем абсолютно каждую анкету. 80 млн поддельных страниц на Facebook и огромное число ненастоящих аккаунтов различных людей в Twitter доверия, согласитесь, не вызывают.

Вероятно, трудно привлечь рекламодателей к «частной» социальной сети.

Как вы справляетесь с этим?

После того, как в 2006 году Харви Вайнштейн купил A Small World, акцент был сделан на обслуживание рекламодателей. С финансовой точки зрения проект пользуется успехом. Например, мы стали первой интернет-площадкой для рекламы Cartier. У нас также размещались Mercedes Benz, Net-A-Porter, Jaguar и многие другие рекламодатели. Однако в последнее время бизнес-модель сдвигается в сторону обслуживания участников сообщества, поэтому рекламы стала меньше и она не столь навязчива.

Лили Квонг, Ида Лоло, Варис Ахлувалиа, Поппи Делевинь и Дерек Бласберг

Что было самым большим сюрпризом для вас в работе над A Small World?

Сюрпризов было много как хороших, так и плохих. Это было действительно удивительно осознавать, насколько участники заботятся о репутации сообщества. Это заставляет меня гордиться работой, которую я делаю.

Многие ли из ваших друзей регулярно используют A Small World?

Да, и меня это радует. Друзья не просто пользуются A Small World, но и могут дать советы, покритиковать, когда надо.

Задача проекта — временно, чтобы сделать мир меньше. Вам не кажется, что эта идея идет вразрез с желанием людей сегодня преувеличивать все, что их окружает?

Плыть против течения — тоже один из наших принципов. Я думаю, доверие и конфиденциальность совсем скоро будут иметь для людей необыкновенную ценность. И тот факт, что все больше людей хотят стать частью A Small World, лишь подтверждает это.

Присоединяйся офлайн к аудиовизуальной инсталляции «Портрет поколения» по случаю 10-летия BURO. — получи иммерсивный опыт.

Купить билет

Игра Small World

Small World – это игра о маленьких народах, ведущих ожесточенную войну за ограниченные территории. В игре участвуют амазонки, дворфы, нежить, крысолюды, колдуны, волшебники и другие расы – все они такие разные, но все отчаянно борются за право на существование и пытаются создать мощную империю. Эта игра появилась 10 лет назад и до сих пор она не теряет своей популярности. Так что же в ней такого особенного?

Small World – это увлекательная стратегия с контролем территорий. Игра соединяет в себе достаточно серьезные механики и легкий, даже слегка озорной подход к жанру в целом. Достаточно разочек взглянуть на персонажей, чтобы всецело проникнуться завораживающей атмосферой этой удивительной игры. SmallWorld – развлечение очень изменчивое. Пока одни расы стремительно набираются сил, другие могут постепенно угасать. Порой лучше перевести ослабленную армию на охрану тыла, а вперед вывести воодушевленных новичков, чем пытаться выжать последнее из своих любимчиков.

Маленький мир – идеальный выбор для начинающих стратегов. Эта игра привлекает простыми правилами, сравнительно быстрыми раундами, приятным художественным оформлением. Игра научит быстро реагировать на смену окружающей ситуации, а умелое использование свойств расы и оперативное переключение с одной расы на другую поможет победить в непростом противостоянии.

Комплектация:

2 двусторонних игровых поля;
6 больших двусторонних памяток;
15 знамён и 21 жетон способностей;
168 жетонов народов;
18 жетонов забытых племён;

10 тролльих пещер;
6 крепостей;
9 гор;
5 лагерей;
2 норы;
2 героя;
1 дракон;
109 монет;
кубик подкреплений;
маркер раунда;
правила игры;
органайзер для компонентов игры.

Правила игры Small World

Обзор дополнения «Small World: Небесные острова» | Игры, Настольные игры

Над Маленьким миром нависла тень, вернее — сразу несколько теней: это приплыли Небесные острова. Их плодородные земли позволяют вступить в игру ещё одному участнику, однако попасть на них можно лишь через Лестницу или Бобовый стебель. И, значит, в Маленьком мире скоро вспыхнет большая война.

«Маленький мир» — прекрасная стратегическая игра, не лишённая, впрочем, некоторых проблем. Из самых серьёзных можно отметить сильную зависимость от порядка ходов и постоянную игру на одном и том же поле, если у вас постоянное число участников. Именно эти проблемы во многом решает новое дополнение.

Small World: Sky Islands

Тип игры: стратегия, дополнение
Авторы: Филипп Кейарт и Т. Алекс Дэвис при участии Сэма Лэссетера
Издатель в России: Hobby World, 2020 год
Количество игроков: 3–6 (оптимальное — 3–4)
Возраст игроков: от 8 лет
Длительность партии: 40–90 минут

Сперва может показаться, что летающие регионы не такое уж значительное нововведение. Согласно правилам, при игре с островами надо использовать основное поле, рассчитанное на меньшее число участников. Но цимес в другом — с «материка» наверх можно попасть только через два региона. Если быстренько их занять и прикрыть, скажем, непробиваемыми хоббичьими норами или героями, то другие игроки окажутся отрезанными от островов. Ну, разве что у них есть способности, позволяющие забраться наверх, вроде полёта или знания тоннелей (как подземные ходы простираются до летающих островов?! Они что, внутри бобового стебля проходят? Загадка!). Кроме того, если одной расой занять остров полностью, он будет приносить дополнительную монетку в каждый ход — бонус хоть и небольшой, но стабильный.

Обе эти новации заметно улучшают положение того, кто ходит первым, — раньше первый ход был не очень приятной обязанностью. Дело в том, что второй игрок практически всегда выбирает какую-нибудь агрессивную расу и с упоением начинает вырезать отряды первопроходца. Острова же позволяют первому игроку в начале заработать чуть больше и укрепиться чуть лучше — особенно при игре на троих, где переходы к островам располагаются относительно близко.

Опять же, хорошо, что в «Маленький мир» благодаря «Островам» можно спокойно поиграть вшестером, не прибегая к подземной версии игры. Впрочем, если вы скупаете ещё не локализованные дополнения, это для вас не новость — уже издавалось отдельное большое поле на шесть человек, да и аддон Realms тоже решал эту проблему. Так что если у вас всё это уже есть, наибольшую ценность для вас составляет не поле, а новые расы и способности.

Новые расы

Вендиго — хороший вариант второй расы для длинной игры, причём чем больше игроков, тем перспективнее эти существа. Раз в ход они могут выкурить из любого леса на карте всех противников, при этом увеличив свою популяцию на один жетон.

Драгоны — прекрасный вариант для быстрого старта. Умеют каждый ход превращать до трёх своих жетонов в драконов — только жетоны при этом сбрасываются. Оптимальная тактика — сделать три жетона на первом ходу, быстро захватить большую территорию и на второй ход уже отправляться «на пенсию».

Падальщики — весьма интересный «второй темп». При захвате региона с расой в упадке не убирают её жетоны, а заключают «договор о коллективной безопасности». При этом очки с региона получаются дважды — и «упадочной» расой, и падальщиками. Идеальное комбо — захватывать регионы со своими же «пенсионерами»: так вы и защищённость регионов повысите, и доходы с них будете получать дважды.

Пугала — их много, но за каждый отбитый у активных пугал регион игрок получает бонусную монетку. Очень сильны в сочетании с какой-нибудь защитной способностью вроде дипломатии, а пугала-оборотни, если выпадет такое сочетание, будут долго преследовать вас в кошмарах.

Улитки — очень специфическая раса, годится для старта, если попадётся со способностью, позволяющей эффективнее захватывать регионы. Улиток много, но деньги они получают не в конце своего хода, а в начале следующего. Воздушные улитки — вариант не хуже, чем пугала-оборотни.

Ханы — пример новой механики, когда на бонусных клетках доходы выше обычного, а на небонусных — нулевые. Конкретно ханы зарабатывают только на полях и холмах. Из русской локализации можно предположить, что за одно поле или холм они получают всего по одной монете, но на самом деле по две: одну за занятый регион и одну бонусную.

Штормовые великаны — лицо дополнения. Могут начинать игру на Небесных островах. Умеют захватывать два горных региона в ход с помощью силы Зевса и всего одного жетона расы. Особенно хороши в борьбе против своих младших братьев-гигантов из оригинальной игры.

Новички интересные — создатели уже в который раз смогли придумать любопытные механики, которые органично вписываются в игру. Нарисованы они тоже неплохо, хотя, безусловно, рисунки уступают в изяществе оригинальным. В исходной версии «Маленького мира» каждая раса и каждая способность были проиллюстрированы каким-нибудь забавным гэгом: эльфы нюхают цветочки; дракона заманивают на нужные клетки, держа перед его мордой привязанного к палке человечка; символ троллей — знак биологической угрозы, поскольку их берлоги отпугивают другие расы ароматом нестиранных носков. В первых дополнениях вроде «Великих Дам» эту традицию ещё удавалось поддерживать, но дальше на неё махнули рукой, и иллюстрации стали просто мультяшно-фэнтезийными. Потому из новых рас «Островов» запоминаются только пугала, чей облик отсылает к снеговику Олафу из «Холодного Сердца».

Больше всего в новом дополнении смущает коробка: из-за карты она такого же формата, как и оригинал, но ей суждено всегда быть на две трети пустой. Так и хочется засунуть туда два пластиковых лотка с другими дополнениями: кажется, что они должны идеально поместиться! Но на деле им не хватает пары сантиметров. Так что если вы перфекционист — приготовьтесь страдать. Радикальным решением проблемы будет убрать карту и правила в основную коробку, а пластиковый лоток с дополнением прихватить аптечными резинками и хранить отдельно — но редкий настольщик готов на такое святотатство.

Новые суперспособности

Воздушные — оборотни на минималках. В ход, когда взята раса с этим свойством, захват территорий требует на два жетона меньше. Идеальная способность для какой-нибудь многочисленной расы на первый ход. На второй уходим в упадок и получаем огромную «пенсию».

Вымогающие — прекрасное свойство для вашей первой расы. Каждый раз, когда кто-то выбирает расу и кладёт монетки за пропуск неугодных вариантов, вы получаете столько же монеток себе. Но главная сила способности не в этом: ваша следующая раса достанется вам совершенно бесплатно, будь она даже шестой в списке!

Дирижабные — вариация способности «берсерк», только в случае выпадения пустой грани на кубике из региона удаляются все жетоны противника (один по традиции погибает), а сам регион становится недоступным на один ход. А ещё в этой аварии вы тоже теряете один жетон! Способность хороша для эльфов и любых рас, которые могут пополнять свои ряды, а для всех прочих риски, пожалуй, перевешивают пользу. Ну, разве что если надо выбить противника из определённого региона любой ценой. Например, потому что у него следующее свойство.

Золотоносные — напоминает способность ханов, но в данном случае деньги приносят только регионы с шахтами — зато три монетки за ход! Опять же, в русской локализации может показаться, что вы получаете две монеты за ход, но не дайте себя обмануть! Золотоносные ханы будут получать по одной монетке с пашен и холмов и по две — с шахт.

Ищущие — единственное свойство в игре, завязанное на, собственно, острова — так что если будете играть с новыми расами, но без самой карты островов, оставьте его в коробке. Для получения максимальной выгоды старайтесь, чтобы число занятых вами регионов на островах и основном материке в конце хода было одинаковым. Работает тем лучше, чем многочисленнее раса.

Сговорчивые — хитрое свойство, позволяющее за деньги защищаться от агрессии других игроков. Всучаете соперникам договор — и за каждую территорию, которую у вас отхапают, получите от них пропорциональное количеству договоров число монет. Штука сильно ситуационная, но каких-нибудь пугал защищает неплохо.

Стрелковые — раса получает две пушки, которые защищают регион и помогают захватывать соседние. Подвох в том, что пушки нельзя быстро перебрасывать: выстрелили, на следующий ход переползли в соседнюю провинцию, подождали ход, снова выстрелили. Подходит для игры «вторым темпом» и в обороне проходов на Небесные острова.

Неплохим вариантом игры для большой компании будет совмещение всех трёх локализованных коробок разом — получится здоровая многоуровневая карта! Да, придётся кое-где идти на компромиссы и затыкать некоторые несоответсвия хоумрулами, но зато какое масштабное приключение получится в итоге! Ну а в условиях самоизоляции можно поиграть втроём, выдав каждому игроку по две расы. Потратите несколько часов, но это будет самая эпичная партия «Маленького мира» в вашей жизни.

ИТОГ: «Небесные острова» помогут вам приятно разнообразить битвы за Маленький мир, особенно если в них регулярно участвует одинаковый состав игроков. Большое количество агрессивных способностей немного повышает динамику, а ограниченность выходов на острова и приятные бонусы за их полный контроль помогают первому игроку на несколько ходов вырваться вперёд. Если оригинальная игра вас всерьёз зацепила — это дополнение достойно вашего внимания.

Купить дополнение «Small World. Небесные острова» на Hobby Games

«Small World».

Персонажи и их свойства. — Funmill — путеводитель по миру настольных игр…

Амазонки. 4 дополнительных жетона ис. В конце каждой Перегруппировки, удалите 4 жетона с поля, убедившись, что в каждом вашем Регионе остался хотя бы один Жетон Расы. Вы можете вновь использовать эти 4 жетона лишь при Подготовке Отрядов в следующий ваш ход.Гномы. Каждый Шахтёрский Регион, занятый вашими Гномами, приносит 1 дополнительную Победную Монету в конце вашего хода. Это свойство действует, даже если Гномы Угасающая Раса.

Вурдалаки. Все ваши Жетоны Вурдалаков остаются на карте, когда Раса становится Угасающей, вместо обычного предела в один Жетон на Регион. В дополнение, сделанные однажды Угасающими, ваши Вурдалаки могут продолжать захватывать Регионы в последующие ходы, как если бы они были Активной Расой. Однако эти завоевания должны выполняться в начале вашего хода, до завоеваний вашей Активной Расы.

Вы даже можете атаковать Угасающими Вурдалаками вашу Активную Расу, если пожелаете.Гиганты. Ваши Гиганты могут захватывать любой Регион со скидкой в один Жетон Гиганта, если этот Регион соседний с Горным Регионом, уже занятым Гигантами. По-прежнему требуется хотя бы один Жетон Гиганта.

Халфинги. Ваши Жетоны Халфлингов могут вводиться на поле с любого Региона карты, не только с крайних. Положите Норы-в-земле в первые два Региона, которые вы захватите. Эти Регионы имеют иммунитет к захвату, так же как и к свойствам Расы и Особых Способностей. Удалите Норы-в-земле(и лишитесь защиты в этих Регионах), когда ваши Халфлинги становятся Угасающей Расой, или если вы решите покинуть Регион, в котором находится Нора-в-земле.Люди. Каждый Фермерский Регион, занятый вашими Людьми, приносит 1 дополнительную Победную Монету в конце вашего хода.

Орки. Каждый «не пустой» Регион, захваченный вашими Орками в этот ход, приносит 1 дополнительную Победную Монету в конце вашего хода.Крысолюди. У них нет особых свойств: одного количества их Жетонов достаточно!

Скелеты. Во время вашей Перегруппировки, возьмите 1 нового Скелета из запаса за каждые 2 «не пустых» Региона, захваченные вами в этот ход, и добавьте их к отряду, которые вы переместили в конце хода. Если Жетонов Скелетов в запасе больше нет, вы не получаете дополнительные Жетоны.Колдуны. В ваш ход, по разу против каждого оппонента, ваши Колдуны могут захватить Регион, заменив один Активный Жетон вашего противника на один ваш собственный, взятый из запаса. Если в запасе больше нет Жетонов, вы не можете захватывать Регионы таким образом. Жетон, заменяемый вашими Колдунами, должен быть единственным в этом Регионе (одинокий Тролль со своим Логовом является при этом единственным, так же как и Жетоны в Крепости или в Горах), и Регион должен быть соседним с вашими Колдунами.

Верните заменённый Жетон Расы противника в запас. Если Эльф заменяется Колдуном, Эльфы отправляют свой Жетон в запас.

Тритоны. Ваши Тритоны могут захватывать прибрежные Регионы (с общей границей с морем или озером), со скидкой в 1 Жетон Тритона. По-прежнему требуется хотя бы один Жетон Тритона.Тролли. Положите Логово Тролля в каждый Регион, занятый вашими Троллями. Логово Тролля увеличивает защиту вашего Региона на 1 (как если бы там ‘лежал ещё один ваш Жетон Тролля), и остаются на поле, даже если Тролли становятся Угасающей Расой. Удалите Логово Тролля, если вы покинули этот Регион или он был захвачен противником.

Волшебники. Каждый Магический Регион, занятый Волшебниками, приносит 1 дополнительную Победную Монету в конце вашего хода.

Поделиться ссылкой:

Понравилось это:

Нравится Загрузка…

Маленький мир Джонатана Эвисона: 9780593184127

Похвала

Выбор Amazon за лучший месяц в литературе и художественной литературе масштаб, наполненный красотой и насилием, трагедией и искуплением. Это такая историческая фантастика, которая не дает спать всю ночь, горит в жилах, как керосин.”— Джейми Форд, New York Times автор бестселлеров Отель на углу горького и сладкого

«Творческое, глубокое художественное произведение. Эвисон проворачивает замечательный акт повествования, на который немногие решались бы, и еще меньше тех, кто смог бы добиться такого резкого результата!» — Джейсон Мотт, автор лауреата Национальной книжной премии Книга «Ад»

«Эвисон придает рассказу живую, захватывающую атмосферу, несмотря на значительный состав актеров, которых он собрал… Не упрощая и не надев розовые очки. , Evison предлагает новый способ узнать наши отношения без шаблонных клише.Сердечная, широкоэкранная американская сказка». —Kirkus Reviews (помечено звездочкой)

«Шедевр… Такие мастерские штрихи, кажется, делают Small World квинтэссенцией великого американского романа, поскольку Эвисон красноречиво показывает, что, возможно, самый аутентичный американский идеал — это продолжающаяся смешанная палитра. историй». — Booklist (помечено звездочкой)

«Каждый кусочек за кусочком, Evison успешно собирает эту обширную историю в единое целое, объединяя ее в яркую мозаику… Во всем этом Evison подчеркивает чувство общей Америки , не столько в мифологии кумбая о плавильном котле, сколько в ощущении — которым в наши дни часто пренебрегают — что мы все вместе участвуем в этом приключении по строительству нации. — BookPage (звездочка)

«Читатели Small World не смогут оторваться от книги. Автор мастерски раскрывает элементы рассказов». — Midwest Book Review

«Честолюбивый… Описание Эвисоном семейных историй персонажей приобретает значимость по мере того, как современное расовое неравенство и классовое неравенство выявляются на фоне тех, что были в 1850-х годах… Насыщено пониманием. — Publishers Weekly

«Новый роман Джонатана Эвисона может стать одной из лучших книг года, а сейчас только январь. Действительно хорошо написанная история, основанная на характере… Вы не захотите оторваться от этой книги. Вы не разочаруетесь.» — Красная ковровая дорожка

Small World by Ishta Mercurio

Детский писатель Ишта Меркурио (Bite Into Bloodsuckers) и иллюстратор I Hatched Джен Корас объединяются, чтобы представить читателям чудесную и красивую иллюстрированную книгу Small World .Поэтический взгляд на меняющуюся перспективу и отношение одной девочки к миру природы по мере ее взросления, Small World отправляет читателей в приключение, которое начинается с утешительных объятий матери и заканчивается внушающим благоговейный трепет взглядом на наш мир. .
Нанда становился все больше и больше. Но по мере того, как она росла, мир рос, t

Детский писатель Ишта Меркурио (Bite Into Bloodsuckers) и иллюстратор I Hatched Джен Корас объединяются, чтобы подарить читателям чудесную и красивую иллюстрированную книгу Small World .Поэтический взгляд на меняющуюся перспективу и отношение одной девочки к миру природы по мере ее взросления, Small World отправляет читателей в приключение, которое начинается с утешительных объятий матери и заканчивается внушающим благоговейный трепет взглядом на наш мир. .
Нанда становился все больше и больше. Но вместе с ней рос и мир. Он превратился в качание ветвей… Стальные леса… И канаты, и шестерни, и дерн, и дерн, и движение по инерции сквозь ночь.
Когда рождается главная героиня этой истории, Нанда, ее мир представляет собой окружность рук ее матери, но по мере того, как она растет, меняется и ее мир, и ее взгляд на мир. «Круг рук ее матери» разрастается до ее семьи, одноклассников, игровой площадки, колледжа… до того, как Нанда растет, загипнотизированная формами, механизмами и, наконец, что не менее важно, воздухоплаванием и КОСМОСОМ! Через каждое большое изменение, через которое проходит Нанда по мере взросления, читатели видят меняющиеся точки зрения Нанды, а также вездесущую и невероятную геометрию форм в мире. Иллюстрации Джен Кораче размеренны, точны и да, совершенно потрясающие: они привлекают внимание читателя и/или слушателя и восхищают тем, как много можно увидеть: геометрические формы, линии, цвета, узоры.Я часто говорю о «соответствии» между автором и иллюстратором и о том, как идеальный щелчок между двумя работами демонстрирует таланты каждого: для Small World великолепно поэтические и вдумчивые, лирические слова Меркурио (уравновешенные нежным, повторяющимся припевом). ) прекрасно запечатлены и освещены карандашом, тушью и гуашью полноцветных изображений Кораче.
В общем, какая чудесная книжка с картинками! Маленький мир задумчивый и чудесный, мощный как в тексте, так и в иллюстрациях. Получатель сильных и отмеченных звездами обзоров, Small World не только говорит о радости от просмотра и просмотра все большего количества книг, связанных с STEAM (и с женскими персонажами!), но также является просто восхитительным, воодушевляющим видом чтения. это может потребовать более пристального взгляда, дальнейших исследований и, возможно, привести к большим и маленьким вопросам о мире. Бонус : не пропустите «Примечание автора» и «Об имени Нанды» в конце книги, . и обязательно загляните на сайт Abrams, чтобы увидеть больше интерьеров из книги!
Я получил копию этого заголовка от автора в обмен на честный обзор и для публикации в блоге.Все мнения и комментарии являются моими собственными.
Сеть малого мира — Scholarpedia
Сеть малого мира относится к ансамблю сетей, в которых среднее геодезическое расстояние (т.е. кратчайший путь) между узлами увеличивается достаточно медленно в зависимости от числа узлов в сети. Этот термин часто применяется к одной сети в такой семье, и термин «сеть маленького мира» также часто используется для обозначения игрушечной сети Уоттса-Строгаца.
Определение
Сеть (или граф ) состоит из узлов (то есть вершин), соединенных ребрами. Путь (или маршрут ) в сети представляет собой последовательность чередующихся узлов и ребер, которая начинается с узла и заканчивается узлом, так что соседние узлы и ребра в последовательности являются инцидентными друг другу (Боллобас, 2001; Ньюман, 2018). Узлы или ребра могут появляться несколько раз в одном и том же пути, а количество ребер в пути равно длине пути .Если граф связен , то любой узел может быть достигнут через путь конечной длины, начинающийся с любого другого узла. Кратчайший путь между парой узлов называется геодезическим путем , и таких путей может быть более одного.
Между любой парой узлов в невзвешенной сети можно вычислить геодезическое расстояние , которое определяется минимальным количеством ребер, которые необходимо пройти, чтобы добраться от начального узла до узла назначения.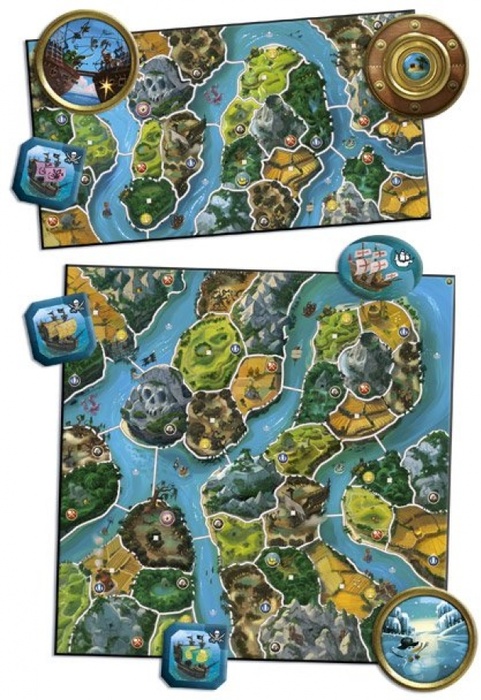 (Можно также рассмотреть направленные и взвешенные обобщения.) Количество ребер в пути равно длине пути. Расстояние от меня до одного из моих друзей равно 1 (поскольку я могу добраться до них через один «скачок» по сети), расстояние от меня до друга моего друга, который не является моим другом, равно 2 и так далее.
Диаметр графа является максимальным из геодезических расстояний между парами узлов, и мир, инкапсулированный графом, является «маленьким», если ожидаемое количество переходов между двумя случайно выбранными людьми в каком-то смысле мало.В частности, говорят, что сеть является сетью малого мира (или удовлетворяет свойству малого мира ), если среднее геодезическое расстояние между парами узлов мало по отношению к общему количеству узлов в сети: обычно желательно, чтобы эта длина \(\ell\) росла не быстрее, чем логарифмически по мере того, как число узлов стремится к бесконечности. То есть \(\ell = O(\log N)\) как \(N \rightarrow \infty\). Основание логарифма значения не имеет.
Важно отметить, что для строгого определения свойства маленького мира необходим ансамбль графов.Многие люди, которые сосредотачиваются на эмпирических данных, находят это неудовлетворительным, поскольку интуитивно может быть желательно рассмотреть, является ли отдельная сеть «маленьким миром», а приведенное выше определение не позволяет этого сделать. (С другой стороны, можно вычислить всю обычную диагностику для эмпирической сети и, таким образом, напрямую изучить ее свойства. Можно также каким-то образом рандомизировать данную сеть и сравнить ее свойства, такие как среднее геодезическое расстояние, со свойствами в ансамбль, созданный в процессе рандомизации.)
Фон
В конце 1920-х годов венгерский писатель Фридьес Каринти написал рассказ под названием Láncszemek (что переводится как Chains или Chain-Links на английском языке), в котором два персонажа считали, что любые два человека на Земле могут быть связаны друг с другом цепочкой не более чем из пяти знакомых (Karinthy, 1929). В 1950-х годах Итиэль де Сола Пул и Манфред Кохен написали рукопись под названием «Контакты и влияние» (де Сола Пул и Кохен, 1978–1979), в которой были сформулированы важные идеи в социальных сетях и включено обсуждение количественной оценки расстояния между людьми через цепочки. соединений.(Эта статья широко распространялась среди ученых в течение многих лет и, наконец, была опубликована в качестве первой статьи — помимо короткой редакционной статьи — в журнале Social Networks в конце 1970-х.) Чтобы проверить существование коротких путей социальных связей между человек, психолог-экспериментатор Стэнли Милграм в 1960-х годах провел знаменательные исследования феномена маленького мира в человеческих социальных сетях (Milgram, 1967; Travers and Milgram, 1969). Милгрэм стремился количественно определить типичную дистанцию между акторами (т.т. е., узлы) в социальной сети и показать, что следует ожидать, что она будет небольшой. Его серия экспериментов была попыткой проверить идею о том, что мир становится все более взаимосвязанным в условиях растущей глобализации.
В одном из своих экспериментов Милграм отправил 96 посылок людям, живущим в Омахе, штат Небраска, США, которых он выбрал «случайным образом» из телефонного справочника. В каждом пакете был официальный буклет с гербом Гарвардского университета (преподавателем которого был Милгрэм).В каждом пакете также были инструкции, согласно которым получатели должны попытаться передать этот буклет конкретному целевому лицу (другу Милгрэма, который жил в Бостоне, Массачусетс, США). Единственной информацией о друге Милгрэма было его имя (и, следовательно, косвенно его пол), его адрес и тот факт, что он был биржевым маклером. Каждому получателю было дано указание отправить посылку кому-то, кого они знали по имени, кто, по их мнению, был бы социально «ближе» к целевому человеку (например,г., имея более схожий род занятий, живя ближе к цели и т. д.). Затем каждый человек, который впоследствии получил один из пакетов, должен был следовать тем же инструкциям, чтобы попытаться доставить пакет к цели.
Цель получила 18 из 96 посылок. Этот показатель успеха оказался выше, чем ожидалось, а современная версия эксперимента Милгрэма, в которой использовалось общение по электронной почте, имела значительно меньший показатель успеха (Dodds, 2003). Милгрэм попросил участников записывать в пакет каждый шаг пути, и среднее количество прыжков пройденных путей составило около 5.9. Это привело к популяризации идеи о том, что между каждой парой людей в мире не более 6 шагов, что выражается фразой «6 степеней разделения». Еще более захватывающим, чем небольшое количество прыжков между людьми, которое обнаружил Милгрэм, является то, что участники его эксперимента демонстрировали легкость, с которой можно было перемещаться по социальной сети, используя очень мало (и в основном локальную) информацию.
Актер Кевин Бэкон невольно стал частью этой истории пару десятилетий назад, когда несколько студентов колледжа, задумав попасть на шоу Джона Стюарта на MTV (Barabási, 2003; Durrett, 2007), по-видимому, решили, что «6 степеней Кевина Бэкон» звучало достаточно похоже на «6 степеней разделения», что должно означать, что Кевин Бэкон был «центром» актерской вселенной. (На самом деле в сетях существует множество представлений о центральности .) У актера есть «число Бэкона» 1, если он появился в фильме с Кевином Бэконом, и число Бэкона 2, если он появился в фильме с кем-то другим. с номером Бэкона 1 и сам не имеет числа Бэкона 1 и т. д.
Математики уже делали что-то подобное много лет назад, так как довольно популярно пытаться найти кратчайший путь от себя к Полу Эрдёшу, который является одним из пионеров теории графов (Hoffman, 1998).Рассмотрим сеть, узлы которой определяются людьми, а невзвешенные ребра указывают на то, что два узла совместно написали как минимум одну статью. (Существуют гораздо более сложные и подходящие способы изучения сетей соавторства, если кто-то хочет исследовать их с научной точки зрения (Leydesdorff, 2001; Newman, 2001a; Newman, 2001b; Redner, 2005).) Затем «числа Эрдеша» определяются аналогично числа Бэкона. Например, я знаю, что мое число Эрдёша не больше 4, потому что я использовал MathSciNet, чтобы найти путь длины 4 между Полом Эрдёшем и мной. Один из таких путей следующий: я написал статью в соавторстве с Шуй-Ни Чоу (у которой число Эрдёша 3), который написал статью в соавторстве с Дэвидом Грином-младшим (номер Эрдёша 2), который написал статью в соавторстве с Цзюцяном. Лю, написавший статью в соавторстве с Эрдёшем. Причина, по которой я прямо заявляю, что мое число Эрдёша ограничено выше 4, заключается в том, что число 4, указанное MathSciNet, использует только места публикации, которые индексируются MathSciNet, поэтому может быть более короткий путь через публикацию, которую он не включает.Это, наряду с экспериментом Милгрэма, привело к идее сетевой навигации. В частности, одно дело констатировать, что геодезические пути в среднем короткие, но, как правило, гораздо сложнее найти короткий путь — и особенно трудно гарантировать, что он найден кратчайший, — без полного знания структуры сети.
Можно также рассчитать число Эрдеша-Бэкона, равное сумме числа Эрдеша и числа Бэкона. Некоторые люди, такие как Натали Портман, имеют низкие числа Эрдеша-Бэкона. (Как описано в статье Википедии о числах Эрдеша-Бэкона, у Портмана есть путь сотрудничества, который включает Джозефа Гиллиса, чье число Эрдеша равно 1.)
Также стоит отметить, что существуют некоторые проблемы с традиционными числами Эрдёша, и были разработаны некоторые обобщения (Morrison, 2010).
Сети Ватт-Строгац
Самое известное семейство сетей малого мира было сформулировано Дунканом Уоттсом и Стивом Строгацем в основополагающей статье 1998 года (Watts and Strogatz, 1998), которая помогла науке о сетях стать популярным средством выражения для многих физиков, математиков, компьютерщиков, и много других.Также есть замечательное интерактивное переосмысление их статьи (Виктор, 2011). Термин «сети маленького мира» (или «модель маленького мира») часто используется для обозначения сетей Уоттса-Строгаца (WS) или их вариантов, хотя многие считают предпочтительным определять малый мир в более общем виде ( как в настоящей статье) (Newman, 2000). Однако в литературе существуют разногласия, поскольку другие (включая первоначальных авторов) предпочитают использовать этот термин для описания сетей как с малой средней длиной геодезического пути, так и со значительной локальной кластеризацией (Watts and Strogatz, 1998). Кроме того, обратите внимание, что исследование графов, удовлетворяющих свойству маленького мира, предшествовало модели Уоттса – Строгаца. Например, (Bollobás and Chung, 1988) содержит доказательство того, что диаметр сети, состоящей из \(N\)-цикла плюс случайное совпадение, масштабируется логарифмически с \(N\) с вероятностью \(1\) как \(N \стрелка вправо \infty\). (Замкнутый путь, который начинается и заканчивается в одном и том же узле, называется циклом .) В сопоставлении один разбивает набор узлов на \(N/2\) пары узлов, если \(N\) четно или состоит из пар узлов \((N-1)/2\) и одного синглтона, если \(N\) нечетно; затем добавляется новое ребро между узлами в каждой из этих пар.
Рис. 1: (а) Кольцевая сеть, в которой каждый узел соединен с одним и тем же числом \(l = 3\) ближайших соседей с каждой стороны. (Эта сеть напоминает одномерную решетку с периодическими граничными условиями.) (b) Сеть Уоттса-Строгаца создается удалением каждого ребра с равномерной независимой вероятностью \(p\) и переподключением его таким образом, чтобы получить ребро между парой узлы, которые выбираются равномерно случайным образом. (c) Вариант Ньюмана-Уоттса сети Уоттса-Строгаца, в котором добавляются «кратчайшие» ребра между парами узлов так же, как в сети WS, но без удаления ребер из базовой решетки.Этот рисунок, появившийся в (Newman, 2003), используется с разрешения Марка Ньюмана и SIAM. Copyright © 2003 Общество промышленной и прикладной математики. Повторно используется с разрешения. Все права защищены.
Чтобы обсудить семейство сетей малого мира Уоттса-Строгаца, нам понадобится понятие кластеризации. Глобальный коэффициент кластеризации равен (Newman, 2003; Newman, 2018; Barrat and Weigt, 2000)\[\begin{equation}\tag{1}. C = \frac{3 \,\,\, \times \mbox{ количество треугольников}}{\mbox{количество соединенных троек}}\,, \конец{уравнение}\]
Рисунок 2: Коэффициент кластеризации \(C\) и среднее геодезическое расстояние \(\ell\) между узлами в варианте Ньюмана-Уоттса модели маленького мира Уоттса-Строгаца как функция вероятности перемонтажа \(p\).Обратите внимание, что существует режим с высокой кластеризацией, но низким средним геодезическим расстоянием. (Для каждого значения \(p\) на этом графике вычисляются значения \(C\) и \(\ell\) как средние по ансамблю сетей NW.) Этот рисунок, появившийся в (Newman, 2003), используется с разрешения Марка Ньюмана и SIAM. Copyright © 2003 Общество промышленной и прикладной математики. Повторно используется с разрешения. Все права защищены.
, где треугольник состоит из 3 узлов, полностью соединенных друг с другом (т.е., 3-клика ) и связная тройка состоит из трех узлов \(\{i,j,k\}\) таких, что узел \(i\) соединен с узлом \(j\) и узлом \(j\) соединен с узлом \(k\). Множитель 3 возникает из-за того, что каждый треугольник считается 3 раза в связной тройке. Коэффициент кластеризации \(C\) показывает, сколько троек на самом деле являются треугольниками. Полный граф, в котором каждая пара узлов соединена ребром, с \(N \geq 3\) узлами дает максимально возможное значение \(C = 1\), так как все тройки также являются треугольниками.Минимальное значение коэффициента кластеризации равно \(C = 0\). Также может быть полезно определить локальный коэффициент кластеризации (Watts and Strogatz, 1998; Newman, 2018), но для нашего обсуждения в этом нет необходимости.
Модель сетей малого мира Уоттса-Строгаца демонстрирует, как построить управляемое семейство игрушечных сетей, которые могут одновременно иметь значительную кластеризацию (то есть то, что социологи могли бы назвать высокой транзитивностью ) и малые геодезические расстояния (Watts and Strogatz, 1998). ; Ньюман, 2003; Ньюман, 2018).Эта модель генерирует семейство невзвешенных, ненаправленных сетей (без собственных ребер или множественных ребер), которые интерполируются между двумя ограничивающими ситуациями. Одна крайность состоит из невзвешенной, неориентированной сети с \(N\) узлами, которые, как вы должны представить, расположены по кругу. Как показано на панели (а) рисунка 1, каждый узел соединен с \(l\) ближайшими соседями с каждой стороны. Этот кольцевой граф, который я буду называть «подложкой» модели WS, представляет собой большой мир, поскольку для перемещения между парой узлов можно совершать только медленные «локальные» шаги.Кольцевой граф имеет ненулевой коэффициент кластеризации \(C\) при условии \(l \geq 2\).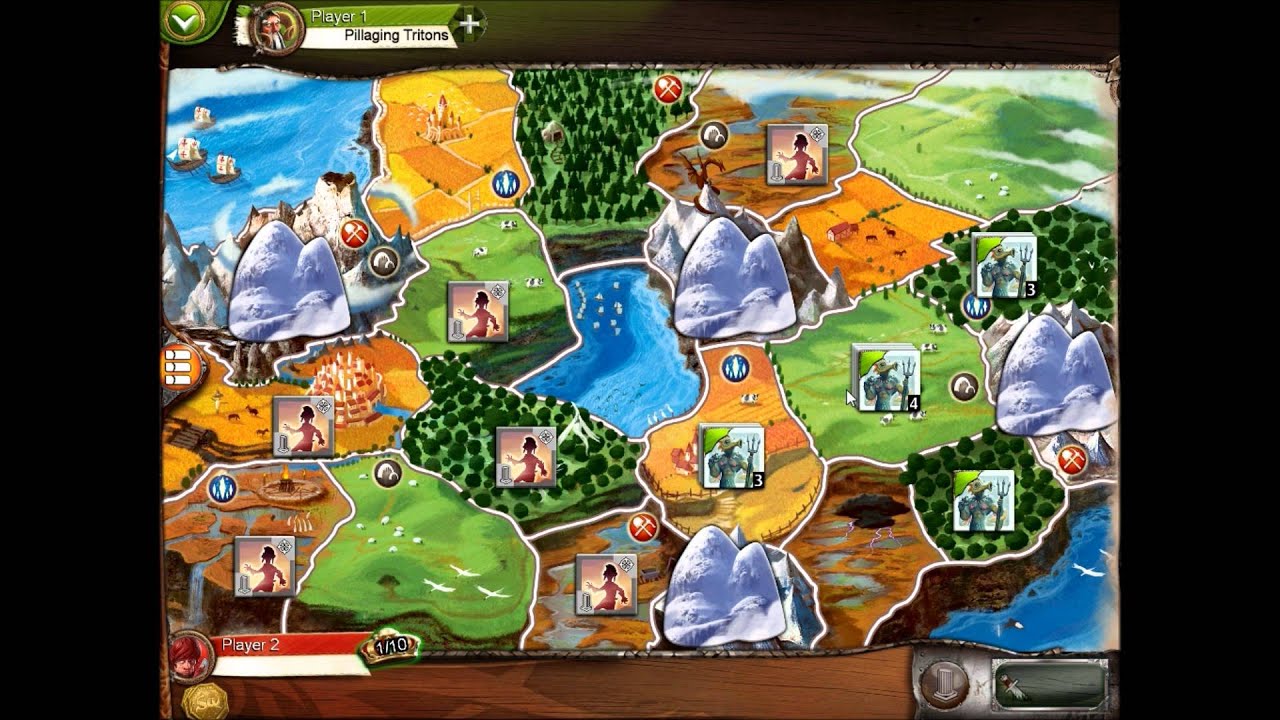 Другой крайностью модели WS является случайный граф Эрдёша-Реньи (ER) , в котором каждая пара узлов имеет равномерную и независимую вероятность соединения друг с другом. Это дает небольшой мир, поскольку обычно можно путешествовать между парой узлов, используя короткий путь. Однако коэффициент кластеризации \(C \rightarrow 0\) как количество узлов \(N \rightarrow \infty.\)
Модель WS, которая параметризована \(p \in [0,1]\), включает режим сетей, которые одновременно демонстрируют как значительную кластеризацию, так и свойство маленького мира.Когда \(p = 0\), мы получаем кольцевой граф, в котором каждый узел связан со своим \(c = 2l\) ближайшими соседями; когда \(p = 1\), мы получаем ER-случайный граф. Как показано на средней панели рисунка 1, \(p\) дает вероятность пересоединения ребра: рассматривается каждое ребро в графе; с независимой и равномерной вероятностью \(p\) это ребро удаляется и заменяется «кратчайшим» ребром между двумя узлами, которые выбираются равномерно случайным образом из \(N\) узлов. (Как обсуждалось в (Newman, 2018), технически это вариант исходной модели WS.) При перемонтаже специально избегают саморебер и мультиребер и сохраняют общее количество ребер. Поскольку модель WS определена вероятностно для \(p \neq 0\), ее изучение влечет за собой изучение ансамбля графов для каждого \(p\) (для фиксированного значения \(N\)). Когда кто-то устанавливает свойство модели WS для фиксированного набора значений параметров (и с \(p \neq 0\)), его следует понимать как среднее значение по ансамблю графов (кроме свойств, которые фиксированы). априори для каждого графа из определения ансамбля).
Одно свойство сети, которое нам нужно рассчитать, — это коэффициент кластеризации. Для \(p = 0\) коэффициент кластеризации равен (Newman, 2018) \(\begin{уравнение} \tag{2} С = \ гидроразрыва {3 (с-2)} {4 (с-1)} \,, \конец{уравнение}\) которое не зависит от количества узлов (пока сеть достаточно велика, чтобы избежать эффекта насыщения конечного размера) и варьируется от \(C = 0\) до \(c = 2\) (т. е. ближайший сосед соединение) с \(C \rightarrow 3/4\) для \(c \rightarrow \infty\). (Точнее, результат \(C \rightarrow 3/4\) остается в силе до тех пор, пока в игру не вступят эффекты конечного размера, потому что \(c\) стало слишком большим по сравнению с \(N\).3 \quad \text{as} \quad N \rightarrow \infty\,. \конец{уравнение}\) Значение \(C\) велико даже при больших значениях \(p\), а значение \(\ell\) мало даже при малых значениях \(p\).
Знаменитая особенность модели WS, а именно наличие большого диапазона \(p\), что позволяет создавать графы маленького мира со значительной кластеризацией, вдохновила многочисленные последующие исследования. Например, в конце 1990-х — начале 2000-х годов появлялись статьи за статьями, в которых исследовались варианты модели Уоттса — Строгаца (Newman, 2000; Newman, 2018).В частности, Ньюман и Уоттс (Newman and Watts, 1999a) ввели вариант семейства сетей WS (см. правую часть рисунка 1), в котором вводятся новые «кратчайшие» ребра точно так же, как в модели WS, но больше не удаляются. края от кольцевой подложки. То есть для каждого ребра в кольце существует независимая равномерная вероятность \(p\) добавления короткого пути между парой узлов, выбранных равномерно случайным образом. Аналогичная модель была предложена одновременно Монассоном (Monasson, 1999).
С помощью численных расчетов видно, что сети WS имеют высокие \(C\) и низкие \(\ell\) для многих значений \(p\), но проверить эти особенности с помощью строгих расчетов непросто. В сети NW кольцо подложки остается нетронутым, что значительно упрощает расчеты. Недостатком является то, что \(C \not\rightarrow 0\) as \(p \rightarrow 1\) (для \(c > 2\)), поскольку в этом пределе больше не получается случайный граф ER. Следовательно, вариант NW модели WS имеет аналогичное поведение для малых и промежуточных значений \(p\), но не для значений \(p\), слишком близких к \(1\) (см. рис. 2).2}\,. \конец{уравнение}\)
Чтобы изучить свойство маленького мира, желательно иметь выражение для среднего геодезического расстояния \(\ell\). {- 1} \ left (\ sqrt {\ frac {x} {x + 4}} \ правильно) \конец{уравнение}\) а \(Ncp\) — ожидаемое количество коротких ребер.2р}\,. \конец{уравнение}\) Другими словами, пока количество сокращений намного больше, чем \(1\), среднее геодезическое расстояние \(\ell\) увеличивается логарифмически с количеством узлов \(N\). То есть эти сети демонстрируют свойство маленького мира.
Интуитивно можно ожидать, что многие реальные социальные сети будут демонстрировать свойство маленького мира (Newman, 2018). (Поэтому, если кто-то каким-то образом может исследовать несколько реализаций подобных социальных сетей, он ожидает логарифмического или более медленного масштабирования среднего геодезического расстояния с количеством узлов.) Сети Уоттса-Строгаца и их варианты обеспечивают управляемые модели, в которых свойство маленького мира и значительная локальная кластеризация проявляются одновременно. Именно это делает их интересными для изучения, хотя ни распределение степеней сетей WS (и подобных им ансамблей), ни их свойства кластеризации не напоминают таковые реальных социальных сетей. Как видно на рисунке 2, масштабирование среднего геодезического расстояния между узлами в маленьком мире может происходить для тех же значений \(p\), при которых локальная кластеризация (и, следовательно, транзитивность) в сети значительна.Иногда, в конце концов, это действительно тесен мир.
Другие примеры
Как я упоминал выше, Ref. (Watts and Strogatz, 1998) привело к огромному количеству последующих работ (Newman, 2000; Strogatz, 2001; Newman, 2018; Newman, 2003), а понятие сетей малого мира оказало огромное влияние как на теорию, так и на Приложения.
Некоторые классы сетей могут создавать особенно маленькие миры. Например, рассмотрим построение невзвешенной ненаправленной случайной сети с заданным распределением степеней (Aiello et al.{1/(\lambda — 1)}\) обеспечивают нижнее и верхнее отсечение для того, что в противном случае является степенной формой. ( степень узла — это количество соединенных с ним ребер, а распределение градусов сети может быть либо определено на основе набора заданных степеней узла, либо задано непосредственно некоторым распределением вероятностей, из которого степени узла рисуются. ) Если \(\lambda \in (2,3)\), то среднее геодезическое расстояние графика \(\ell \sim a_0\ln \ln N\) для некоторой постоянной \(a_0\) (Коэн и Havlin, 2003; Дороговцев и др.д\). Кроме того, идея «наименьшей» сети малого мира была исследована в (Nishikawa et al. , 2002), а важность малости сети малого мира для динамических систем в сетях обсуждалась в (Melnik ). и др. , 2011).
Самым удивительным аспектом экспериментов Милгрэма было не то, что мир тесен, а то, что люди, казалось, очень хорошо ориентировались в маленьком мире с почти полностью локальной информацией. (См. мои комментарии выше относительно моей попытки найти короткий путь бумажного соавторства между Полом Эрдёшем и мной.) Чтобы исследовать сетевую навигацию, Джон Клейнберг изучил сообщений, проходящих по сетям (Kleinberg, 2000; Easley and Kleinberg, 2010; Newman, 2018). Клейнберг ввел модель, подложкой которой является кольцо узлов со связью ближайших соседей. Он включил географические эффекты, предположив, что узлы вокруг кольца знают, насколько они близки друг к другу. Короткие пути по-прежнему располагаются между парами узлов случайным образом, но теперь конкретную пару узлов выбирают так, чтобы вероятность того, что конкретный короткий путь покроет расстояние \(r\) (т.{-\alpha}\), где \(\alpha \geq 0\) — параметр смещения, а нормирующая постоянная \(K\) гарантирует, что у одного есть четко определенная вероятность. При размещении короткого пути сначала выбирают расстояние \(r\) из распределения вероятностей, а затем помещают короткий путь между парой узлов (выбранных равномерно случайным образом), которые находятся на расстоянии ровно \(r\) прыжков друг от друга на кольце. . Предельный случай \(\alpha = 0\) дает модель NW. Когда \(\alpha > 0\), предпочтительно выбираются соединения между соседними узлами, и эффект становится тем сильнее, чем больше \(\alpha\).
Есть, конечно, и многое другое. Например, один интересный вопрос заключается в том, в каких сетях легко ориентироваться, используя только локальную информацию, и можно также спросить, как вообще может возникнуть масштабирование маленького мира (Clauset and Moore, 2003, Mogren et al. , 2009).
Каталожные номера
В. Айелло, Ф. Чанг, Л. Лу. Модель случайного графа для степенных графов. Экспериментальная математика 10 , 53–66 (2001).
А.-Л. Барабаши. Связано: Новая наука о сетях , Perseus Books, Нью-Йорк (2003).
А. Баррат, М. Вейт. О свойствах сетей малого мира. Европейский физический журнал B 13 , 547–560 (2000).
М. Бискуп. Диаметр графика в дальнодействующей перколяции. Случайные структуры и алгоритмы 39 (2), 210–227 (2011).
Б. Боллобас. Современная теория графов , Academic Press, Нью-Йорк (2001)
Б.Боллобас, ФРК Чанг. Диаметр цикла плюс случайное совпадение. Журнал SIAM по дискретной математике 1 , 328–333 (1988).
Ф. Чанг, Л. Лу. Средние расстояния в случайных графах с заданными ожидаемыми степенями. Труды Национальной академии наук 99 , 15879–15882 (2002).
А. Клаузе, К. Мур. Как сети становятся судоходными? ArXiv: cond-mat/0309415 (2003).
Р. Коэн, С. Хавлин. Безмасштабные сети очень малы. Письма о физическом обзоре 90 , 058701 (2003 г.).
Р. Коэн, С. Хавлин. Сложные сети: структура, надежность и функции , издательство Кембриджского университета, Кембридж (2010).
П. С. Доддс, Р. Мухамад, Д. Дж. Уоттс. Экспериментальное исследование поиска в глобальных социальных сетях. Наука 301 , 827–829 (2003).
С. Н. Дороговцев, Ж. Ф. Ф. Мендес, А. Н. Самухин. Метрическая структура случайных сетей. Nuclear Physics B ‘ 653 , 307–338 (2003).
Р. Дарретт. Random Graph Dynamics , Cambridge University Press, Кембридж (2007).
Д. Исли, Дж. Клейнберг. Сети, толпы и рынки: рассуждения о мире с высокой степенью связи . Издательство Кембриджского университета, Кембридж (2010).
П. Хоффман. Человек, который любил только числа: история Пола Эрдёша и поиски математической истины , Гиперион, Нью-Йорк (1998).
Ф. Каринти. «Звенья цепи», в Все по-другому .[Переведено с венгерского и аннотировано Адамом Маккаем. Под редакцией Энико Янко. Доступно онлайн на этом сайте.] (1929).
Дж. Клейнберг. Навигация в маленьком мире. Природа 406 , 845 (2000).
Л. Лейдесдорф. Проблема наукометрии , Universal Publishers, Бока-Ратон (2001).
С. Мельник, А. Хакетт, М. А. Портер, П. Дж. Муха, Дж. П. Глисон. Необоснованная эффективность древовидной теории для сетей с кластеризацией. Physical Review E 83 , 036112 (2011).
С. Милграм. Проблема маленького мира. Psychology Today 1 (1), 60–67 (1967).
О. Могрен, О. Сандберг, В. Верендель, Д. Дубхаши. Адаптивная динамика реалистичных сетей малого мира. ArXiv: 0804.1115 (2008 г.).
Р. Монассон. Законы диффузии, локализации и дисперсии на решетках «малого мира». Европейский журнал физики B 12 , 555–567 (1999).
Г. Моррисон, Л. Махадеван. Обобщенные числа Эрдеша. ArXiv: 1010.4293 (2010).
М. Э. Дж. Ньюман, Модели маленького мира. Журнал статистической физики 101 , 819–841 (2000).
М. Э. Дж. Ньюман. Сети научного сотрудничества: I. Построение сети и фундаментальные результаты. Physical Review E 64 , 016131 (2001).
М. Э. Дж. Ньюман. Сети научного сотрудничества: II. Кратчайшие пути, взвешенные сети и центральность. Physical Review E 64 , 016132 (2001).
М. Э. Дж. Ньюман. Структура и функции сложных сетей. SIAM Review 45 (2), 167–256 (2003).
М. Э. Дж. Ньюман. Networks , второе издание, Oxford University Press, Оксфорд (2018).
М. Э. Дж. Ньюман, К. Мур, Д. Дж. Уоттс. Решение среднего поля сетевой модели маленького мира. Письма с физическим обзором 84 , 3201–3204.
М.Э. Дж. Ньюман, Д. Дж. Уоттс. Ренормализационный анализ сетевой модели маленького мира. Письма по физике A 263 , 341–346 (1999).
М. Э. Дж. Ньюман, Д. Дж. Уоттс. Масштабирование и перколяция в сетевой модели маленького мира. Physical Review E 60 , 7332–7342 (1999).
Т. Нишикава, А. Э. Моттер, Ю.-К. Лай, ФК Хоппенстедт. Самая маленькая сеть в маленьком мире. Physical Review E 66 , 046139 (2002).
С. Реднер. Статистика цитирования журнала Physical Review за 110 лет. Physics Today 58 , 49–54 (2005).
И. де Сола Пул, М. Кохен. Контакты и влияние. Социальные сети 1 , 5–51 (1978–1979).
С. Х. Строгац. Изучение сложных сетей. Природа 410 , 268–276 (2001).
Дж. Трэверс, С. Милграм. Экспериментальное исследование проблемы маленького мира. Социометрия 32 , 425–443 (1969).
Б. Виктор. Научная коммуникация как последовательное искусство (2011).
Д. Дж. Уоттс, С. Х. Строгац. Коллективная динамика малых сетей из . Природа 393 (1), 440–442 (1998).
Внутренние ссылки
Следующие статьи Scholarpedia имеют отношение к настоящему обсуждению:
Рекомендуемое чтение
Соответствующую информацию можно найти в следующих книгах и статьях (и во многих других ресурсах):
М.Э. Дж. Ньюман. Структура и функции сложных сетей. SIAM Review 45 (2), 167–256 (2003).
М. Э. Дж. Ньюман. Сети, второе издание, издательство Оксфордского университета, Оксфорд (2018).
С. Х. Строгац. Изучение сложных сетей. Природа 410 , 268–276 (2001).
Д. Дж. Уоттс, С. Х. Строгац. Коллективная динамика сетей «маленького мира». Природа 393 (1), 440–442 (1998).
См. также
Дополнительные онлайн-источники, представляющие интерес, включают:
С.Форман, Оракул бейсбола, доступен в Интернете.
П. Ламер, 6 степеней Black Sabbath, доступно онлайн.
MathSciNet, Collaboration Distance, доступно онлайн.
Дж. Дж. О’Коннор, Э. Ф. Робертсон, Биография Пола Эрдёша, доступна в Интернете.
П. Рейнольдс, Оракул Бэкона, доступен в Интернете.
Б. Виктор. Научная коммуникация как последовательное искусство, доступно в Интернете (2011 г.).
У. Виленски, Java-апплет NetLogo для сетей Уоттс-Строгац, доступен в Интернете.
Запись в Википедии о комплексной сети, доступная онлайн.
Запись в Википедии о номере Эрдеша-Бэкона, доступна в Интернете.
Запись в Википедии для Network Science, доступная онлайн.
Запись в Википедии о теории сетей, доступная онлайн.
Запись в Википедии о шести степенях Кевина Бэкона, доступная в Интернете.
Запись в Википедии об эксперименте в маленьком мире, доступная онлайн.
Запись в Википедии для Small-World Network, доступна онлайн.
Запись в Википедии о модели Уоттса-Строгаца, доступна в Интернете.
Благодарности
Я благодарю Марка Ньюмана за разрешение использовать рисунок 1 и рисунок 2, а также выражаю признательность Сету Бромбергеру, Рику Дарретту, Мартину Эверетту, Джеймсу Глисону, Кресо Йосичу, Дэвиду Кемпе, Дженнифер Китсон, Дэвиду Кракхардту, Вито Латора, Эндрю Линцу, Борису Мотику. , Питеру Мухе, Оливеру Риордану и Стиву Строгацу за полезные комментарии к этой статье.
Как играть в Маленький мир | Официальные правила

Компоненты
2 двусторонних игровых поля
14 фантастических гонок с соответствующими баннерами и жетонами
20 значков особой силы
10 логовищ троллей, 9 гор, 2 дыры, 6 крепостей, 5 лагерей, маркер игрового хода
2 героя и 1 дракон
109 монет победы
6 листов со сводками игроков
1 Укрепляющая матрица
1 Буклет с правилами

Настройка
Выберите карту, соответствующую количеству игроков, и положите ее на стол.
Поместите маркер игрового хода на первую точку трека игрового хода на карте.
Трек используется для отслеживания хода игры. Игра заканчивается в конце хода, когда маркер игрового хода достигает последней позиции на треке.
Поместите лоток со всеми расами рядом с игровым полем в пределах досягаемости всех игроков.
Перемешайте все знамёна рас и вытяните 5 (случайно) и положите их лицевой стороной вверх в одну колонку.
Поместите оставшиеся баннеры лицевой стороной вверх в одну стопку внизу колонны.
Проделайте то же самое со значками особой силы и разместите по одному слева от знамени каждой расы.
Сложите остальные значки стопкой слева от стопки знамен гонки.
Поместите жетон Затерянного племени в каждую область карты с символом Затерянного племени.
Эти цивилизации уже пришли в упадок, но все еще населяют некоторые территории карты.
Поместите жетон горы на каждую область карты с горой.
Дайте каждому игроку по пять монет победы (из 1). Поместите все оставшиеся монеты, включая все «3», «5» и «10» рядом с доской. Эти монеты будут служить вашей валютой во время игры и помогут определить победителя в конце.
Объект игры
Пространство в Маленьком Мире становится тесным, и слишком много рас живут за пределами земли.
Выбрав фантастическую комбинацию Расы и Особой Силы, вы должны использовать их уникальные расовые черты и навыки, чтобы завоевать соседние территории и собрать победные монеты для каждого региона, который вы занимаете в конце своего хода.
В конце концов, ваша раса станет чрезмерно многочисленной, и вам придется покинуть свою цивилизацию и искать другую. Очень важно знать, когда подтолкнуть свою гонку к упадку и начать новую гонку к превосходству.

Игра
Выберите игрока, чтобы начать игру. Этот игрок перемещает маркер игрового хода вперед на одно деление по шкале игрового хода и делает свой ход.
Затем игра продолжается по часовой стрелке, и как только все игроки сделали ход, начинается новый ход.Когда маркер игрового хода достигает последней отметки, разыгрывается последний ход, и игра заканчивается.
Игрок с наибольшим количеством победных монет побеждает в игре.

I. Первый поворот
Во время 1-го хода игры каждый игрок:
Комбинация «Выбор расы и особой силы»
Игрок выбирает одну расу и комбинацию особой силы из шести, видимых на столе.
Стоимость каждой комбинации определяется ее позицией в столбце.Первая комбинация (верхняя часть столбца) бесплатна. Каждая следующая комбинация (сверху вниз) стоит одну дополнительную монету, и игрок оплачивает эту стоимость, бросая одну монету на все вышеперечисленные комбинации.
Если комбинация содержит монеты Победы (выпавшие из предыдущих игроков), игрок берет эти монеты, но все равно платит за эту комбинацию.
Теперь игрок выбирает количество подходящих жетонов расы, равное сумме значений, указанных на флаге расы и связанном с ним значке особой силы.
Даже если Особая Способность позволяет вам брать дополнительные жетоны Расы из лотка для хранения, вы все равно ограничены общим количеством физически доступных жетонов.
Наконец, игрок пополняет столбец комбо, доступных другим. Это достигается за счет перемещения существующих комбо на одну позицию вверх и открытия новой комбинации с вершины стека.
Завоевание регионов
Жетоны расы игрока используются для завоевания регионов или территорий на карте.
Первое завоевание
Раса игрока, впервые размещающаяся на карте, должна попасть на нее, завоевав один из приграничных регионов.
Завоевание региона
Чтобы завоевать регион, игрок должен иметь в наличии для развертывания:
Два жетона гонки.
1 дополнительный жетон Расы за каждый маркер Лагеря, Крепости, Горы или Логова Тролля.
1 дополнительный жетон расы за каждый уже присутствующий в регионе жетон.
Моря и озера обычно невозможно завоевать.
Игрок должен разместить жетоны расы, которые он использовал для завоевания этого региона, внутри его границ на карте.
Эти жетоны должны оставаться в этом регионе до тех пор, пока игрок не реорганизует свои войска в конце этого хода.
Потери и отступления противника
Если жетоны расы другого игрока занимали регион до его завоевания, этот игрок должен немедленно забрать все эти жетоны расы и:
навсегда сбросить один жетон расы обратно в лоток для хранения.
сохраните жетоны другой расы и перераспределите их в любом другом регионе (регионах), все еще занятых его расой.
Регион(ы), в котором передислоцируются оставшиеся жетоны Расы, не обязательно должен быть смежным или смежным с регионом(ами), из которого они сбежали.
Если все регионы игрока были атакованы в этом ходу, и у него не осталось жетонов расы на поле, он может перераспределить их, как если бы он совершал первое завоевание на своем следующем ходу.
Когда регион, защищаемый одним жетоном, захвачен, то жетон защиты сбрасывается (обычно, когда защитник является Затерянным Племенем или принадлежит к расе, находящейся в упадке.
Примечание: Игрок может захватить регион, занятый его собственным жетоном «Упадок». Горы неподвижны и остаются на месте, чтобы обеспечить защиту своему новому завоевателю.
После завоеваний
Активный игрок может повторить этот процесс, чтобы завоевать столько новых регионов, сколько он пожелает в свой ход (когда останется достаточно жетонов расы).
Каждый из недавно завоеванных регионов должен быть смежным с регионом, уже занятым его активными жетонами Расы (если только это не разрешено комбинацией Расы/Особой Силы).
Бросок кубика «Последняя попытка завоевания/Подкрепление»
Во время последней попытки завоевания в свой ход игрок может обнаружить, что у него недостаточно жетонов Расы, чтобы сразу завоевать другой Регион.
При условии, что у него все еще есть хотя бы один неиспользованный жетон Расы, игрок может попытаться выполнить последнее завоевание за свой ход, выбрав регион, для завоевания которого ему обычно не хватает 3 или менее жетонов Расы.
Этот регион не обязательно должен быть самым слабым из доступных, его все же можно завоевать удачным броском кубика.
Если сумма выпавших кубиков в сочетании с оставшимися у него жетонами расы достаточна для завоевания Региона, игрок размещает оставшиеся жетоны расы там.
В противном случае он размещает оставшиеся жетоны в одном из регионов, которые он уже занимал ранее.
Передислокация войск
Как только завоевания игрока на этом ходу закончились, он может свободно перераспределять жетоны расы, которые у него есть на поле, перемещая их из одного региона в любой другой, занятый его расой.
Нет необходимости, чтобы эти регионы были смежными.

Монеты победы
По завершении хода игрок получает по 1 монете из победного тайника за каждый регион, занимаемый его жетонами расы на карте.
Игрок также может получить дополнительные Победные монеты в результате преимущества Расы и/или Особой Силы.
Регионы, в которых находятся жетоны в упадке, также приносят игроку по одной победной монете, но знамя расы и особые способности больше не приносят бонусных монет, если иное прямо не указано в преимуществах расы или особой силы.
Игроки прячут свои победные монеты. Окончательные результаты не раскрываются до конца игры.
II. После поворотов
В следующие ходы первый игрок перемещает маркер игрового хода на одну позицию вверх по шкале, и игра продолжается по часовой стрелке.
Во время своего хода каждый игрок должен:
Расширение за счет новых завоеваний
Готовь свои войска
Оставив на месте по одному жетону расы в каждом занимаемом регионе, игрок может взять все остальные активные жетоны расы с карты и использовать их для завоевания новых регионов.
Завоевать
Все правила, касающиеся завоевания нового региона, должны соблюдаться, за исключением правила, касающегося первого завоевания, которое применяется только к новым расам, появившимся на карте.
Выход из региона
Только те жетоны Расы, которые были возвращены в руки, могут быть использованы для завоевания новых регионов.
Если игрок хочет освободить еще несколько жетонов расы, он может полностью очистить некоторые или все регионы, не оставив там жетонов.
Эти теперь заброшенные регионы больше не будут считаться его и больше не будут давать монеты Победы.
Если игрок отказывается от всех регионов, его следующее завоевание должно следовать тем же правилам, что и его первое завоевание.
Вход в упадок
Если игрок считает, что его активная раса слишком растянулась и не может продолжать успешно расширяться, он может поставить ее в упадок, выбрав новую комбинацию расы и особой силы из доступных на столе в начале своего следующего повернуть.
Игрок переворачивает свое знамя текущей расы вверх ногами, чтобы серая сторона «В упадке» стала видна всем, и сбрасывает связанный с ним значок особой силы, поскольку этот значок особой силы больше не действует, если не указано иное ( например, особая сила духа).
Он также переворачивает один жетон расы стороной «В упадке» в каждом регионе, который занимают эти жетоны, и удаляет с карты все остальные жетоны этой расы.
У каждого игрока может быть только одна раса в состоянии упадка на карте в любой момент времени.
Если у игрока все еще остались жетоны более ранней расы в упадке, оставшиеся на карте, все они немедленно удаляются с карты.
Знамя расы ныне исчезнувшей расы помещается в нижнюю часть стопки знамен рас или в самую нижнюю пустую ячейку в столбце знамен.
Игрок не может совершать завоевания во время хода, когда его раса приходит в упадок, и его ход заканчивается сразу после подсчета очков!
Он получает 1 Победную монету за каждый регион, который занимают его новые жетоны Упадка, но, если не указано иное, он не получает Победных монет за силу знамени расы, которая теперь находится в Упадке, или сброшенные особые способности.
На следующем ходу игрок выберет новую расу и комбинацию особых способностей. Затем он следует тем же правилам, что и в первый ход игры. Единственное отличие состоит в том, что теперь игрок, скорее всего, будет собирать Победные монеты из своей новой расы, а также из оставшихся жетонов его расы, находящейся в упадке.
В том маловероятном случае, если в стеке особых способностей не останется достаточно значков особой силы, чтобы продолжать добавлять новые комбинации расы и особой силы на стол, перетасуйте ранее сброшенные значки особой силы в новую колоду.

Конец игры
: Как только маркер игрового хода достигает своей последней отметки на треке игрового хода и все игроки имеют возможность сыграть последний ход, открываются победные монеты.
Побеждает игрок с наибольшим количеством очков. В случае ничьей побеждает игрок с наибольшим количеством жетонов гонки (активных + в упадке) на доске.

Продолжить чтение
сообщить об этом объявлении
«это маленький мир» Отдых в Диснейленде: 7 советов для первого путешествия
После недавнего наводнения, которое вызвало задержку открытия сезона, «это маленький мир» Праздник в Диснейленде теперь принимает гостей снова в радостные путешествия. Вот семь советов, которые помогут вам впервые испытать праздник «Мир тесен» в Диснейленде.
Пришло время отпраздновать и, наконец, отправиться в «Самый веселый кругосветный круиз». Первоначально запланированное к открытию 11 ноября 2021 года, с наложением сезонных праздников, «это маленький мир» в Диснейленде имел одну большую проблему: . За день до своего дебюта аттракцион фа-ла-ла-ла затопило!
Машины и механизмы этого любимого аттракциона пострадали от наводнения, из-за чего его закрытие продлилось. Наконец, 6 декабря произошло праздничное чудо — «Этот маленький мир» снова открылся благодаря тяжелой работе преданных своему делу участников.
Правильно: гости Диснейленд-парка наконец-то снова могут насладиться праздником «Мир тесен».
О празднике «Мир тесен» в Диснейленде
Не пропустите Праздник «Мир тесен» в Диснейленде. Photo by Brian Shih
«Этот мир тесен» Holiday — моя любимая праздничная смесь классики культуры и новых технологий , делающая каждый год лучше, чем предыдущий. А теперь мы можем добавить «затопило… плохо» к списку «этот мир тесен». Праздничные факты, которые мы вспоминаем каждую зиму.
Диснейленд «Этот мир тесен» Праздник является обязательным для посещения гостями парка каждый год , и с каждым годом он становится все лучше и лучше. Ниже мы составили подробный путеводитель по Празднику «Этот маленький мир» для тех, кто впервые посетил .
Ваш путеводитель по Диснейленду «Мир тесен» Праздник
Вы впервые в Диснейленде на каникулах ? Добавьте праздничный оверлей «Маленький мир» в свой список.Вот что вам нужно знать.
Когда появится праздничная оверлей «Этот мир тесен»?
Специальная праздничная накладка для Диснейленда «Этот маленький мир» действует весь день с 6 декабря 2021 г. по 9 января 2022 г. . Его планировалось открыть в ноябре, но у погоды были другие планы.
Да, праздничный оверлей «маленький мир» открыт и днем. Фото Тины Чиу
Сколько ждать?
Время ожидания отпуска «Мир тесен» в Диснейленде может меняться.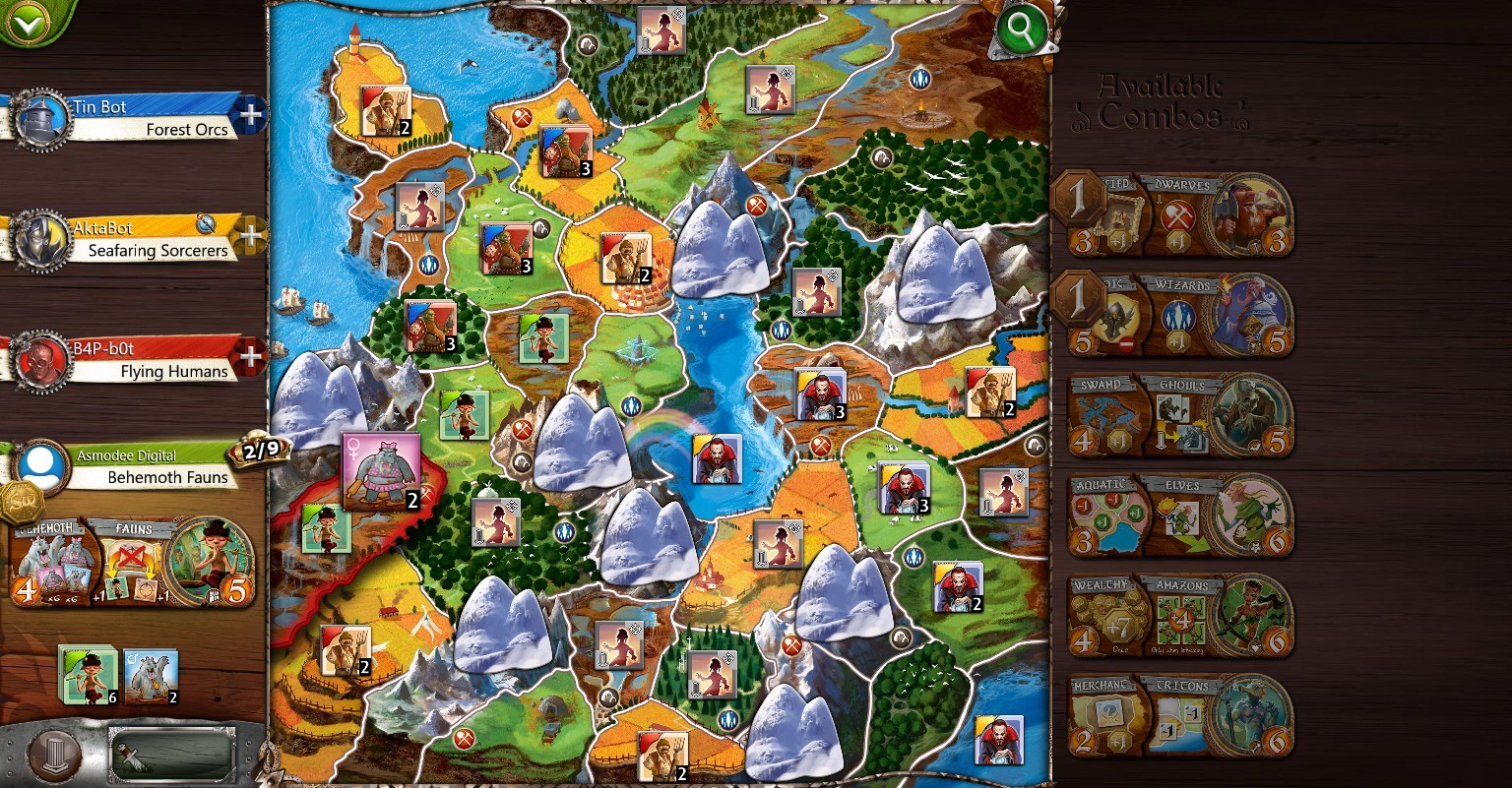
Совет 1. Самый простой способ обойти очередь — использовать Genie+ , которая, наконец, была запущена в Диснейленде 8 декабря.
Каждый год Диснейленд преображает классический аттракцион «Мир тесен» причудливым декором , праздничными мелодиями и светящимся фасадом . Всего 10 сцен демонстрируют уникальные культурные традиции праздника.
Совет 2: Внимательно слушайте «Jingle Shells by the South Sea mermaids; это нравится толпе.
Эти огни 😍 Фото Брайана Ши
Площадь Fantasyland приобретает чудесное сияние с 50 000 огней, освещающих фасад аттракциона, и дополнительных 350 000 мини-светильников , разбросанных по изгородям, деревьям и деревьям. «это маленький мир.»
Совет 3: Если у вас нет времени кататься на «мир тесен», отправляйтесь на улицу, чтобы полюбоваться красивыми огнями.
Компания Disney добавила в путешествие новых иммерсивных аромата , чтобы сделать гостей еще более приятными во время кругосветного плавания. Вы почувствуете ароматы цветов вишни , корицы и кокоса , а также традиционные ароматы прошлых лет сосны и мяты .
Совет 4: Не забывайте во время поездки полагаться не только на зрение. Специальное праздничное наложение использует музыку и запахи, чтобы создать праздничное настроение.
Внутри столько праздничных ароматов! Фото Брайана Ши
Хотите слепить снеговика? Как насчет 14-футового снеговика , сидящего на вершине снежинки шириной 10 футов?
Совет 5: Ищите этого удивительного снеговика в финальной комнате праздника «Мир тесен».Снеговик сделан из сверкающих кристаллов и огоньков.
Снеговик — это шоу-стоппер. Фото Тины Чиу
Наконец, есть табличка с надписью «Счастливых праздников», которая отправляет вас в путь с духом этого праздничного времени года.
С праздником! Фото Тины Чиу
«Мир тесен» Праздник: что еще нужно знать
Вот еще два совета, которые могут оценить новички:
Совет 6: Каждый день в сумерках собираются рядом «Этот мир тесен», чтобы увидеть праздничное световое шоу с 3D-проекциями. Всю ночь на аттракцион будут накладываться проекции.
Совет 7: Вы можете посмотреть Рождественский парад фантазий с тротуаров «этот маленький мир». Если вы сможете занять место, вас ждет настоящее удовольствие в этом месте. Грандиозный праздничный фасад является отличным фоном для фото. Это также одно из самых ярких мест для съемки или фотографирования этого парада . Смотрите «Рождественскую фантазию» в 15:00 и 17:30.
Не уверен, что идешь? Вы можете просто получить больше информации о потенциальных каникулах Диснея.
Знаешь свои даты?

Пока нужен совет?
СЕЙЧАС ОТКРЫТО: Plaza Point Holiday Shoppe at Disneyland Resort
Диснейленд запускает Disney Genie и Genie+ 8 декабря
Повсеместное распространение сетей Small-World
Открытие в сетевой науке. В своей знаменательной статье 1998 года Уоттс и Строгац описали сети, которые «сильно сгруппированы, как регулярные решетки, но имеют небольшую характерную длину пути, как случайные графы» (Уоттс и Строгац, 1998).Другими словами, сети малого мира обладают уникальной способностью иметь специализированные узлы или регионы внутри сети (например, компьютерная сеть с группой машин, предназначенных для определенной задачи), одновременно демонстрируя общую или распределенную обработку на всех взаимодействующих узлах. узлы в сети (например, все компьютеры разделяют рабочую нагрузку). После этой оригинальной статьи многие сети были описаны как демонстрирующие свойства маленького мира, включая такие разнообразные системы, как Интернет, социальные группы и биохимические пути.Учитывая уникальные возможности обработки или передачи информации сетей малого мира, жизненно важно определить, является ли это универсальным свойством естественных сетей или свойства малого мира ограничены специализированными сетями. Чрезмерно либеральное определение «маленького мира» может упустить конкретные преимущества этих сетей — высокую степень кластеризации и малую длину пути — и скрыть их от сетей, более тесно связанных с регулярными решетками и случайными сетями.
Текущее принятое определение сети малого мира состоит в том, что она имеет кластеризацию, аналогичную регулярной решетке, и длину пути, аналогичную случайной сети.Однако на практике сети обычно определяются как «маленькие миры» путем сравнения кластеризации и длины пути с сопоставимыми случайными сетями (Хамфрис и др., 2006). К сожалению, это означает, что сети с очень низкой кластеризацией могут быть определены и действительно определяются как сети с малым миром. Мы предполагаем, что такой метод не может отличить настоящие сети малого мира от тех, которые более тесно связаны со случайными или решетчатыми структурами, и переоценивает возникновение сетей маленького мира.Сети, которые больше похожи на случайные или решетчатые структуры, интересны сами по себе, но они не ведут себя как сети маленького мира. Наличие метрики, позволяющей точно охарактеризовать сети как сети малого мира, случайные или решетчатые, или, по крайней мере, тенденции к одному из этих типов сетей, является чрезвычайно важным фактором в изучении науки о сетях. В этой статье мы определяем новую метрику, которая дает количественную оценку свойств малого мира и помещает рассматриваемую сеть в континуум от решетки к маленькому миру и к случайному.Эта новая метрика ясно демонстрирует, что сети малого мира не так распространены, как сообщается, и предполагает, что многие системы, изначально считавшиеся способными обрабатывать данные в маленьком мире, на самом деле могут таковыми не быть.
Идентификация сетей малого мира
Сети малого мира отличаются от других сетей двумя специфическими свойствами, первым из которых является высокая кластеризация (C) среди узлов. Математически C — это доля ребер e _i , существующих между соседями конкретного узла ( i ), по отношению к общему количеству возможных ребер между соседями (Bullmore and Sporns, 2009). Уравнение для C в отдельном узле степени k _i :
[1]
Общая кластеризация в сети может быть определена путем усреднения кластеризации по всем отдельным узлам. Высокий уровень кластеризации поддерживает специализацию, поскольку локальные наборы сильно взаимосвязанных узлов легко обмениваются информацией или ресурсами. Концептуально кластеризация довольно проста для понимания. По аналогии с реальным миром кластеризация представляет вероятность того, что друзья одного человека также являются друзьями друг друга.
Сети малого мира также имеют короткую длину пути ( L ), что обычно наблюдается в случайных сетях. Длина пути — это мера расстояния между узлами в сети, рассчитанная как среднее кратчайших геодезических расстояний между всеми возможными парами узлов:
[2]
где d _ij — кратчайшее геодезическое расстояние между узлами i и j .
Небольшие значения L обеспечивают легкое распространение информации или ресурсов по сети. Это свойство делает возможной распределенную обработку информации в технологических сетях и поддерживает шесть степеней разделения, о которых часто сообщается в социальных сетях.
Десятилетия исследований установили, что короткая длина пути является характеристикой случайных графов, а высокая кластеризация — свойством решетчатых сетей. Уоттс и Строгац разработали сетевую модель (модель WS), которая привела к созданию первых в мире сетей с кластеризацией, близкой к решетчатой, и длинами путей, подобными случайным сетям.Модель WS демонстрирует, что случайное изменение небольшого процента ребер в решетке приводит к резкому уменьшению длины пути, но лишь незначительному уменьшению кластеризации (). В этой вероятности перемонтажа существует диапазон, в котором несоответствие между кластеризацией и длиной пути очень велико, и именно в этой области реализуются преимущества сетей малого мира.
Модель маленького мира Уоттса и Строгаца. Смоделированная решетка из 1000 узлов со средней степенью k =10 была перемонтирована с различной вероятностью p в диапазоне от 0 до 1. При малых значениях p в сети наблюдается мелкомирность сети с одновременной высокой кластеризацией (квадраты) и малой длиной пути (кружки).
При исследовании свойств малого мира стало обычным сравнивать как кластеризацию, так и длину пути интересующей сети с теми же показателями из эквивалентной случайной сети. В 2006 году Хамфрис и его коллеги ввели количественную метрику, коэффициент малого мира σ , который использует отношение кластеризации сети и длины пути по сравнению с его случайным сетевым эквивалентом (Хамфрис и др., 2006). С тех пор этот показатель приобрел значительную популярность (Bassett et al., 2008; Guye et al., 2010; Liu et al., 2008), особенно среди нейробиологов (Bullmore and Sporns, 2009). 2008). В этом количественном подходе C и L сравниваются с их эквивалентными производными случайными сетями ( C _rand и L _rand соответственно) для получения соотношений γ =
9 /
C _рэнд и λ = л/л _рэнд . Эти отношения затем используются для расчета малого коэффициента как:
[3]
Условия, которые должны быть выполнены для того, чтобы сеть была классифицирована как малый мир: σ >1. Коэффициент маленького мира использовался для приписывания свойств маленького мира многочисленным сетям, начиная от энергосистемы и заканчивая сетью акторов (Humphries and Gurney, 2008).
Сравнение длины пути со случайной сетью имеет смысл — длина пути в сети малого мира должна быть короткой, как и в случайной сети.Однако сравнение кластеризации с эквивалентной случайной сетью не отражает должным образом поведение маленького мира, потому что кластеризация в сети маленького мира более точно имитирует кластеризацию решетчатой сети. Кроме того, общепризнано, что кластеризация в исходной сети намного больше, чем в случайной сети. Но насколько больше должно быть это скопление, чтобы оно напоминало решетку? Если случайная сеть имеет C _rand 0,001, в среднем между соседями узла присутствует только 1 из каждых 1000 возможных соединений. Если исходная сеть имеет C в пять-десять раз больше, чем C _rand , все равно существует только от 5 до 10 каналов из 1000 возможных соединений. Этот низкий уровень кластеризации был показан в сетях (Humphries and Gurney, 2008; Newman 2003) и иллюстрирует уровень кластеризации, обычно не рассматриваемый для решетчатой сети. Тем не менее, разница величин между C и C _rand показывает, что исходная сеть не является полностью случайной сетью.Однако, учитывая низкую кластеризацию, также неясно, в какой степени эта сеть считается малым миром. Интересно отметить, что даже самая ранняя оценка свойств малого мира в реальных сетях сравнивала кластеризацию со случайной сетью (Watts and Strogatz, 1998).
Как оказалось, основная проблема с σ заключается в том, что коэффициент кластеризации эквивалентной случайной сети сильно влияет на коэффициент маленького мира. В коэффициентном уравнении малого мира (3) σ использует отношение между C и C _rand для определения значения γ . Поскольку кластеризация в случайной сети, как правило, чрезвычайно низка (Хамфрис и Герни, 2008; Уоттс и Строгац, 1998), на значение γ могут чрезмерно влиять только небольшие изменения в C _rand . Рассмотрим две сети, A и B , с одинаковой длиной пути, но разными коэффициентами кластеризации 0,5 и 0,05 соответственно. Если оба коэффициента кластеризации эквивалентных случайных сетей равны 0,01, то сеть A явно обладает более высокими свойствами маленького мира.Однако, если кластеризация случайных сетей для A и B составляет 0,01 и 0,001 соответственно, то две сети будут иметь аналогичные значения σ . Интерпретация σ предполагает, что обе сети имеют одинаковые характеристики маленького мира, хотя сеть B имеет значительно более низкую кластеризацию. Хотя верно то, что по сравнению с сопоставимыми случайными сетями эти две сети имеют одинаковые значения σ , они явно имеют разные уровни кластеризации, и сеть A кажется более близкой к решетке, чем сеть . Б .Это открытие происходит потому, что C _rand находится в знаменателе уравнения для γ ; таким образом, небольшие изменения в C _{rand и} в конечном итоге определяют значение σ .
Сравнение кластеризации со случайной сетью накладывает несколько ограничений на использование σ . Например, значения σ находятся в диапазоне от 0 до ∞ и зависят от размера рассматриваемой сети (Хамфрис и Герни, 2008). Более крупные сети с аналогичной кластеризацией и длиной пути, как правило, имеют более высокие значения σ , чем их меньшие аналоги.Наконец, может быть полезно знать, имеет ли сеть свойства, которые имеют тенденцию быть более похожими на решетку или случайными. Невозможно определить эти свойства, если кластеризация и длина пути сравниваются со случайным эквивалентом. Важно определить, демонстрируют ли сети определенное поведение, например специализацию (решетки) или способность эффективно передавать информацию (случайные сети). Мы исследовали новую метрику для количественной оценки свойств малого мира, ω , которая устраняет все ограничения, описанные в предыдущих абзацах, и больше соответствует исходному описанию сетей малого мира, определенному Уоттсом и Строгацем.
«Мир тесен» (Поездка)
Ты уже слышишь, не так ли?
«Когда мы завершили показ фильма «Этот маленький мир» на Всемирной выставке в Нью-Йорке, мы почувствовали, что достигли того, к чему стремились. Мы хотели способствовать лучшему взаимопониманию между народами мира, показывая платье , обычаи, язык, музыка и немного культуры наших соседей по всему миру, и мы хотели показать, что это очень счастливо Я думаю, можно с уверенностью сказать, что веселье имеет универсальную привлекательность.»
— Walt Disney
It’s a Small World (стилизованный под «это маленький мир» ) — водная темная поездка в тематических парках Диснея, оформленная в виде лодочной прогулки по разным странам.
История аттракциона началась в начале 1960-х годов, когда он был одним из многих аттракционов Диснея, созданных для Нового 1964 года. York World’s Fair, а также замечательных моментов с Mr.Lincoln , Carousel of Progress и Magic Skyway . Первоначально аттракцион должен был называться «Дети мира», и первоначальная идея заключалась в том, что на нем будут звучать одновременно национальные гимны разных стран мира, но, протестировав его, Уолт почувствовал, что это не так. работающий. Желая создать одну песню, которую можно было бы легко перевести и многократно воспроизводить, он попросил братьев Шерман придумать лучшее, что у них есть, и так родилась песня.Мэри Блэр, арт-директор, которая ранее сотрудничала с Disney в нескольких их фильмах, также сыграла важную роль в разработке аттракциона, следя за его декорациями и цветовым стилем.
После открытия аттракцион имел ошеломляющий успех у публики, в результате чего в 1966 году он был перенесен в Диснейленд, а в течение следующих нескольких десятилетий он также попал в Волшебное Королевство, Токийский Диснейленд, Диснейленд Париж и Гонконгский Диснейленд.
По сей день аттракцион является одним из самых узнаваемых аспектов парков Диснея, что, естественно, привело к тому, что он стал предметом многочисленных упоминаний и ироничных пародий в средствах массовой информации, в том числе сделанных Сами Диснеи.Популярность аттракциона также привела к тому, что среди прочего появилась большая линейка товаров и онлайн-мультсериал.
Фильм для аттракциона анонсирован в 2014 году; никаких подробностей с тех пор не сообщалось.
Тропы, показанные в
It’s a Small World , включают:
все строчные буквы: Как уже упоминалось, название аттракциона обычно пишется как «это маленький мир» с кавычками вокруг него. (Эй, аттракцион назван в честь его песни.)
Удивительные разноцветные дикие животные: Варьируется. Некоторые из животных окрашены в обычный цвет, в то время как другие окрашены в фиолетовый, синий, оранжевый, красный, розовый… любой цвет, который вы можете себе представить.
Амазонка: Среди многих мест есть тропический лес Новой Гвинеи, где обитатели леса держат зонтики, чтобы защитить себя.
Американцы — ковбои: Единственный американский персонаж, которого можно увидеть в некоторых версиях аттракциона (не считая одинокого эскимоса), по какой-то причине фактически наряжается в стереотипную ковбойскую одежду, которая встречается только в последней части аттракциона.
Парк развлечений: финал происходит в небольшом парке развлечений с колесами обозрения, американскими горками и полетами на воздушном шаре.
Мультяшное животное с аксессуарами: все танцующие пингвины на сцене Антарктиды носят чилийские широкополые шляпы.
Воздушный шар: многие куклы в поездке можно увидеть парящими в воздухе с помощью всего лишь пары воздушных шаров. Одна из кукол в парижском Диснейленде — это ребенок, которого унес воздушный шар, две куклы лежат на земле, одна встревожена, а другая тщательно целится гарпуном, чтобы взорвать его, прежде чем ребенок поднимется слишком высоко.
Такт: Музыка достигает крещендо, затем наступает такт тишины, затем музыка продолжается. Причина этого в том, что оригинальная звуковая система использовала десятки кассетных дек, воспроизводящих лупы. Было бы невозможно синхронизировать их все в течение всего дня; некоторые будут работать быстрее или медленнее и выпадут из синхронизации. Решение состоит в том, чтобы все магнитофоны остановились в конце цикла, а затем одновременно перезапустились по тактовому сигналу. Это поддерживало их синхронизацию, и тишина сопровождала перезапуск.
Большие жуткие ползуны: на Гавайях можно увидеть несколько огромных бабочек, летающих вокруг.
Разрушение четвертой стены: то же самое с падением титула.
Камея:
Текущие версии в Калифорнии, Токио и Гонконге включают версии «маленького мира» персонажей Диснея в соответствующих областях. Некоторые из них действительно очевидны (Ариэль и Лило и Стич в тропиках, Три кабальеро в Южной Америке), некоторые не так очевидны (вам особенно нужно искать Питера Пэна и Динь-Динь, летящих над головой в Европе, и это может занять некоторое время). минуту, чтобы понять, что среди животных джунглей есть Симба, Пумба и Тимон).Кроме того, в азиатских аттракционах есть некоторые персонажи, которых нет в версии Анахайма, такие как Прекрасный Принц и Моана, Хейхей и Пуа.
Камея персонажа, не относящегося к Диснею, в версии для Анахайма — на одной из почтовых марок ближе к концу аттракциона изображено улыбающееся лицо Чарли Брауна среди детей в лодке.
Цивилизованное животное: Зигзаг. Некоторые животные в поездке изображены нормально, в то время как другие показаны очень похожими на людей, стоящими на задних лапах и играющими на музыкальных инструментах, а некоторые даже в одежде.
Башня с часами: Фасад аттракциона представляет собой гигантскую башню с часами с движущимся смайликом; который будет отображать текущее время каждые 15 минут.
Специальное рождественское предложение: It’s a Small World Holiday , оверлей, проводимый в ноябре-январе, который не только добавляет рождественские украшения, но и заставляет куклы петь рождественские песни вместе с основной песней.
Комичное косоглазие: В версии Диснейленда Дори выглядит косоглазой.
Крутая лодка: в первой сцене Диснейленда «Добро пожаловать» показано множество уникальных лодок, приплывающих со всего мира, большинство из которых соответствует стилю своих стран.
Камея создателя: Художественный руководитель аттракциона Мэри Блэр можно увидеть в образе куклы на сцене Западной Европы.
Костюм культурных равных: используется как основной способ визуально различать культуры; см. отвращение к профилированию лица ниже.
Одетый для грабежа: Среди многих вещей в сцене «Добро пожаловать» в Диснейленде есть свинья, одетая как типичный пират, в капитанскую шляпу и пальто.
Кислотная последовательность Disney: каждая комната аттракциона
Эффект Эйфелевой башни: многие достопримечательности используются в аттракционе для обозначения определенных мест, например, Биг-Бен для Соединенного Королевства, Эйфелева башня для Франции и Пизанская башня Пиза для Италии.
Парижская версия идет еще дальше и включает в себя Статую Свободы, Эмпайр Стейт Билдинг, мост Золотые Ворота и Голливудские холмы, представляющие Соединенные Штаты.
В версии для Гонконга есть все вышеперечисленное (за исключением Голливудских холмов), гондола для Венеции, Италия, Тадж-Махал для Индии и центральная сторона гавани Виктория с пиком на заднем плане (в комплекте со звездным паромом и джонка) для самого Гонконга.
С обезьянами все лучше: Обезьяны, кажется, являются наиболее представленными животными в аттракционе, особенно они довольно заметно появляются в африканской сцене.
С радугами все лучше: В сцене Ирландии в парижской версии радуга выходит из горшка с золотом.
С блестками все становится лучше: большая часть аттракциона имеет очень высокое соотношение блесток к общей площади поверхности, особенно на фасаде.
Танцуют Все: Улыбки и танцы не ограничиваются только детьми и животными.
На сцене Соединенного Королевства есть пара танцующих шахматных фигур.
В парижской версии несколько кактусов танцуют; некоторых из них можно даже увидеть играющими на музыкальных инструментах.
Лицо Солнца: почти в каждой сцене есть солнце; у некоторых из них есть лица.
Профилирование лица: предотвращено. Одна и та же форма используется для изготовления лиц для всех кукол, независимо от их этнической принадлежности. Это, конечно, совершенно преднамеренно, поскольку идея, продвигаемая аттракционом, заключается в том, что люди по сути одинаковы, независимо от того, откуда они.
Фантастическая Флора: Танцующие кактусы, как упоминалось выше.
Пушистые модные перья: их носят несколько кукол, особенно танцовщицы канкана во Франции.
Джинн в бутылке: сцена Ближнего Востока в парижской версии показывает девушку, выпускающую джинна из волшебной лампы.
Хула и Луаус: на Гавайях есть несколько танцоров хула.
Гиена: Настоящая гиена появляется в африканской сцене и смеется точно так же, как гиена в Леди и Бродяга .
Джаз в джунглях: слушайте внимательно, иначе вы пропустите, в конце африканского крыла в Волшебном королевстве и Токийском Диснейленде есть заглавная песня, которую в этом стиле играют трое детей, сидящих на бивнях слона.
Лепрекон: Сцена в Ирландии (естественно) показывает лепреконов среди ирландских детей.
Живые игрушки: Фасад башни с часами аттракциона украшен деревянными игрушечными солдатиками, которые будут появляться сбоку каждые 15 минут и играть в свои барабаны.
Long-Runners: в 2014 году аттракциону исполнилось 50 лет, и он по-прежнему актуален и по сей день.
Человек на Луне: фасад парижской версии имеет полусолнце/полумесяц с лицом.
Ковер-самолет: Сцена Ближнего Востока включает в себя несколько кукол, катающихся на коврах-самолетах над головой.
Национальные стереотипы о животных: несколько стран, участвующих в аттракционе, представлены, среди прочего, своим национальным животным. В гонконгской версии, по крайней мере, представлены кенгуру и ее малыш для Австралии, киви для Новой Зеландии, тигр для Индии, панда для Китая, верблюд для Ближнего Востока, множество животных, обитающих в саванне (например, зебры, гиены, слоны, носороги, бегемоты, жирафы и др. ) для Африки, ламы (или что-то в этом роде) для Анд в Южной Америке и пингвины (предположительно, магеллановы пингвины, хотя окраска больше похожа на пингвинов) для предположительно южной оконечности континента, корова (предположительно горная корова) для Шотландии и т. д.
Красивая шляпа: Невероятное количество кукол в аттракционе носят замысловатые шляпы, обычно соответствующие стране.
Панды для публики: панды используются в аттракционе в качестве основных животных, представляющих Китай.
Scenery Porn: большая часть дизайна аттракциона была разработана Мэри Блэр, которая ранее работала над фильмами Диснея, включая The Three Caballeros , Melody Time , Cinderella и Alice in Wonderland , привносит свою яркую торговую марку цвета для езды.
Shout-Out: в парижской версии Диснейленда Лохнесское чудовище смотрит в перископ моряка, что является отсылкой к ныне несуществующему аттракциону World of Motion компании EPCOT.
Заклинатель змей: Сцена на Ближнем Востоке показывает человека, гипнотизирующего змею с помощью флейты.
Зрелищное вращение: В каждой сцене аттракциона всегда есть какая-то форма вращения, обычно исходящая от кукол, танцующих по кругу. Даже на самом фасаде аттракциона есть несколько постоянно вращающихся объектов.
Стокгольмское чудовище: Улыбающееся Лохнесское чудовище появляется в сцене «Добро пожаловать» в Диснейленде.
Sugar Bowl: Действие происходит на красочной земле, где все едины и живут в мире, а также все время счастливы.
Слоган: «Присоединяйтесь к самому счастливому круизу, который когда-либо совершался вокруг света».
Получение титула: буквально на протяжении всей поездки.
Обновленное переиздание: версии аттракциона «Диснейленд» и «Токийский Диснейленд» были изменены в 2009 и 2018 годах, соответственно, чтобы персонажи Disney и Pixar были добавлены в разные сцены аттракциона. В случае с Диснейлендом сцена тропического леса также была сжата в угол другой комнаты и заменена сценой США.
Дикий Запад: США. Сцены в Париже, Гонконге и Анахайме. Версии аттракциона изображают страну времен Старого Запада, полную ковбоев и коренных американцев.До того, как он был обновлен, единственные представители США в Диснейленде (а также в Мире Уолта Диснея и Токийском Диснейленде) были представлены в финале аттракциона с ковбоем и вождем индейцев.
Мировое турне: Поездка доставит гостей со всего мира.
Земля Йодль: Швейцария в этом аттракционе представлена несколькими большими часами с кукушкой и парой кукол, исполняющих йодль под мелодию песни.
Приносим извинения, если чтение этой страницы заставило вас начать напевать эту песню .
.